题目内容
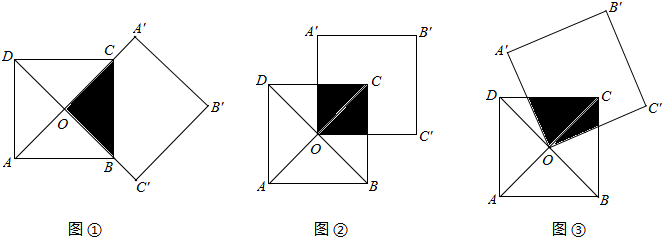
如图,四边形ABCD和四边形A′B′C′O都是边长为2cm的正方形,AC与BD交于点O,将正方形A′B′C′O绕点O按逆时针旋转,其中阴影部分为两正方形的重叠部分.
(1)当点O、A、A′在同一直线上时(如图①)阴影部分面积为______.
(2)当O A′⊥AB时(如图②)阴影部分面积为______.
(3)当O A′与AB不垂直相交时(如图③)请你猜想阴影部分的面积是多少?并证明你的结论.
(4)根据以上信息你能得到什么结论?
解:(1)如图:∵四边形ABCD是正方形,
∴OC=OB= BD,BD⊥AC,∠DAB=90°,
BD,BD⊥AC,∠DAB=90°,
∵正方形ABCD的边长为2cm
∴BD= =2
=2 (cm),
(cm),
∴OC=OD= cm,
cm,
∴S阴影=S△BOC= ×OB×OC=
×OB×OC= ×
× ×
× =1(cm2);
=1(cm2);
(2)∵四边形ABCD和四边形A′B′C′O都是边长为2cm的正方形,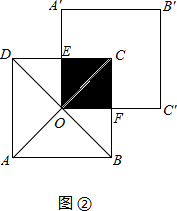
∴OA=OC,AB∥CD,BC=DC=2cm,∠BCD=90°,
∵O A′⊥AB,
∴OA′⊥CD,
∴∠CEO=∠EOC′=∠ECF=90°,
∴四边形EOFC是矩形,
∴OE∥AD,OF∥AB,
∴OE:AD=OC:AC=OF:AB,
∴OE= AD=1(cm),OF=
AD=1(cm),OF= AB=1(cm),
AB=1(cm),
∴OE=OF,
∴四边形EOFC是正方形,
∴S阴影=S正方形EOFC=OE•OF=1(cm2);
(3)1cm2.
证明:∵四边形ABCD和四边形A?B?C?O都是正方形,
∴OA=OB,∠OAE=∠OBF=45°,∠AOB=∠A?OC?=90°,
∴∠AOE=∠BOF,
∴△AOE≌△BOF,
∴S△AOE=S△BOF,
∴S阴影=S△AOB=1cm2;
(4)正方形A?B?C?O绕点O无论怎样移动,两个正方形重叠部分的面积总等于一个正方形面积的 (或正方形A?B?C?O绕点O无论怎样转动,阴影部分的面积总等于1cm2)
(或正方形A?B?C?O绕点O无论怎样转动,阴影部分的面积总等于1cm2)
故答案为:(1)1cm2;(2)1cm2.
分析:(1)由四边形ABCD和四边形A′B′C′O都是边长为2cm的正方形,易求得OC与OB的长,继而求得阴影部分面积;
(2)首先根据题意证得四边形EOFC是正方形,则可求得阴影部分面积;
(3)首先证得△AOE≌△BOF,然后利用(1)的结论,即可求得答案;
(4)结论为:正方形A?B?C?O绕点O无论怎样移动,两个正方形重叠部分的面积总等于一个正方形面积的 .
.
点评:此题考查了旋转的性质、正方形的性质以及等腰直角三角形性质.此题难度适中,注意数形结合思想的应用,注意旋转中的对应关系.
∴OC=OB=
 BD,BD⊥AC,∠DAB=90°,
BD,BD⊥AC,∠DAB=90°,∵正方形ABCD的边长为2cm
∴BD=
 =2
=2 (cm),
(cm),∴OC=OD=
 cm,
cm,∴S阴影=S△BOC=
 ×OB×OC=
×OB×OC= ×
× ×
× =1(cm2);
=1(cm2);(2)∵四边形ABCD和四边形A′B′C′O都是边长为2cm的正方形,

∴OA=OC,AB∥CD,BC=DC=2cm,∠BCD=90°,
∵O A′⊥AB,
∴OA′⊥CD,
∴∠CEO=∠EOC′=∠ECF=90°,
∴四边形EOFC是矩形,
∴OE∥AD,OF∥AB,
∴OE:AD=OC:AC=OF:AB,
∴OE=
 AD=1(cm),OF=
AD=1(cm),OF= AB=1(cm),
AB=1(cm),∴OE=OF,
∴四边形EOFC是正方形,
∴S阴影=S正方形EOFC=OE•OF=1(cm2);
(3)1cm2.
证明:∵四边形ABCD和四边形A?B?C?O都是正方形,
∴OA=OB,∠OAE=∠OBF=45°,∠AOB=∠A?OC?=90°,
∴∠AOE=∠BOF,
∴△AOE≌△BOF,
∴S△AOE=S△BOF,
∴S阴影=S△AOB=1cm2;
(4)正方形A?B?C?O绕点O无论怎样移动,两个正方形重叠部分的面积总等于一个正方形面积的
 (或正方形A?B?C?O绕点O无论怎样转动,阴影部分的面积总等于1cm2)
(或正方形A?B?C?O绕点O无论怎样转动,阴影部分的面积总等于1cm2)故答案为:(1)1cm2;(2)1cm2.
分析:(1)由四边形ABCD和四边形A′B′C′O都是边长为2cm的正方形,易求得OC与OB的长,继而求得阴影部分面积;
(2)首先根据题意证得四边形EOFC是正方形,则可求得阴影部分面积;
(3)首先证得△AOE≌△BOF,然后利用(1)的结论,即可求得答案;
(4)结论为:正方形A?B?C?O绕点O无论怎样移动,两个正方形重叠部分的面积总等于一个正方形面积的
 .
.点评:此题考查了旋转的性质、正方形的性质以及等腰直角三角形性质.此题难度适中,注意数形结合思想的应用,注意旋转中的对应关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.