题目内容
如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，已知∠AP′B=135°，P′A：P′C=1：3，则P′A：PB=（ ）
A． 1：
B． 1：2 C． 
：2 D． 1：
解答： 解：如图，连接AP，∵BP绕点B顺时针旋转90°到BP′，
∴BP=BP′，∠ABP+∠ABP′=90°，
又∵△ABC是等腰直角三角形，
∴AB=BC，∠CBP′+∠ABP′=90°，
∴∠ABP=∠CBP′，
在△ABP和△CBP′中，
∵
，
∴△ABP≌△CBP′（SAS），
∴AP=P′C，
∵P′A：P′C=1：3，
∴AP=3P′A，
连接PP′，则△PBP′是等腰直角三角形，
∴∠BP′P=45°，PP′=PB，
∵∠AP′B=135°，
∴∠AP′P=135°﹣45°=90°，
∴△APP′是直角三角形，
设P′A=x，则AP=3x，
根据勾股定理，PP′=
=
=2
x，
∴PP′=PB=2x，
解得PB=2x，
∴P′A：PB=x：2x=1：2．
故选B．
练习册系列答案
相关题目
如图，△ABC是等腰直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′的长等于（ ）A、3
| ||
B、2
| ||
C、4
| ||
D、3
|
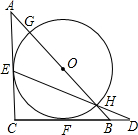如图，△ABC是等腰直角三角形，AC=BC=a，以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F，与AB分别相交于点G、H，且EH的延长线与CB的延长线交于点D，则CD的长为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、(
|
22、已知如图，△ABC是等腰直角三角形，∠C为直角．
如图，△A1A2B是等腰直角三角形，∠A1A2B=90°，A2A3⊥A1B，垂足为A3，A3A4⊥A2B，垂足为A4，A4A5⊥A3B，垂足为A5，…，An+1An+2⊥AnB，垂足为An+2（n为正整数），若A1A2=A2B=a，则线段An+1An+2的长为（ ）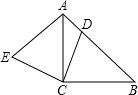
已知：如图，△ABC是等腰直角三角形，D为斜边AB上任意一点（不与A，B重合），连接CD，作EC⊥DC，且EC=DC，连接AE．