��Ŀ����
��ͼ��OABC��һ������ƽ��ֱ������ϵ�еľ��Σ�OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=3��OC=4��ƽ���ڶԽ���AC��ֱ��m��ԭ��O��������x����������ÿ��1����λ���ٶ��˶�����ֱ��m�����OABC�����߷ֱ��ڵ�M��N��ֱ���˶���ʱ��Ϊt(��)��
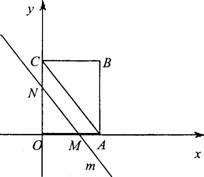
(1)д����B�����ꣻ
(2)tΪ��ֵʱ��MN=![]() AC��
AC��
(3)���OMN�����ΪS����S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ����tΪ��ֵʱ��S�����ֵ?����S�����ֵ��
(1)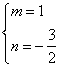
(2)ֱ��PC�Ľ���ʽ��y=![]() x-
x-![]()
(3) �Ե�AΪԲ�ġ�ֱ��Ϊ5��Բ��ֱ��PC���룮
��������
����������⣺(1)����֪������֪��������y=![]() x2+mx+n����A(-3,0)��B(1,0)����.
x2+mx+n����A(-3,0)��B(1,0)����.
�� 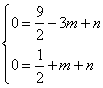 ���
��� 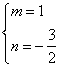
��y=![]() x2+x-
x2+x-![]() .
.
(2)��y=![]() x2+x-
x2+x-![]()
��P(-1��-2)��C-![]() ��
��
��ֱ��PC�Ľ���ʽ��y=kx+b���� 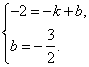 ���
��� 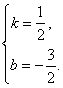
��ֱ��PC�Ľ���ʽ��y=![]() x-
x-![]() ��
��
(3)��ͼ������A��AE��PC������ΪE.
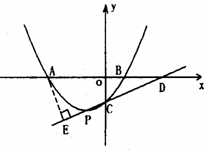
��ֱ��PC��x�ύ�ڵ�D�����D������Ϊ(3,0)
��Rt��OCD����OC=![]() ��OD=3��
��OD=3��
��CD=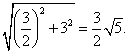
��OA=3��OD=3����AD=6��
�ߡ�COD=��AED=90�㣬��CDOΪ�����ǣ�
���COD����AED��
��![]() =
=![]() ,��
,��![]() =
=![]() .
.
��AE=![]() .
.
��![]() ��2.688��2.5,
��2.688��2.5,
���Ե�AΪԲ�ġ�ֱ��Ϊ5��Բ��ֱ��PC���룮
���㣺������
�����������Ѷ��еȣ���Ҫ����ѧ���Զ��κ�����������ͼ��֪ʶ������ա�Ϊ�п��������ͣ�Ҫ��ѧ���ι����գ�ע�����ν��Ӧ�á�

 ���ڵ�M��N��ֱ���˶���ʱ��Ϊt���룩��
���ڵ�M��N��ֱ���˶���ʱ��Ϊt���룩��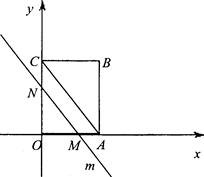
 AC��
AC�� AC��
AC��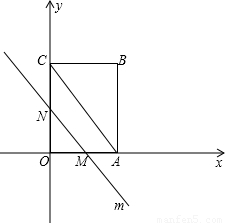
 AC��
AC��