题目内容
如图，⊙O1和⊙O2内切，它们的半径分别为3和1，过O1作⊙O2的切线，切点为A，则O1A的长是________．
分析：连接过切点的半径，构造直角三角形，根据两圆内切，得到两圆的圆心距，再根据勾股定理进行计算．
解答：
解：连接O2A，根据切线的性质，得∠O2AO1=90°，
根据两圆内切，得O1O2=3-1=2，
根据勾股定理，得O1A=
．点评：此题综合运用了切线的性质、勾股定理以及根据两圆内切，正确计算两圆的圆心距的知识点．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
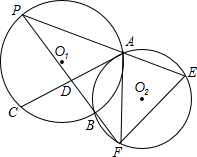
20、已知：如图，⊙O1和⊙O2相交于A、B两点，动点P在⊙O2上，且在⊙1外，直线PA、PB分别交⊙O1于C、D，问：⊙O1的弦CD的长是否随点P的运动而发生变化？如果发生变化，请你确定CD最长和最短时P的位置，如果不发生变化，请你给出证明．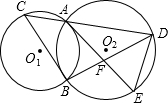
长⊙O1相交于C点，连接BC，过A点作AE∥BC与⊙O相交于E点，与BD相交于F点．
、PB的延长线分别交⊙O2于点E、F，PB交AC于D．
16、如图．⊙O1和⊙O2外切于点A，BC是⊙O1和⊙O2的公切线，B、C为切点，求证：AB⊥AC．
（2001•黄冈）已知，如图，⊙O1和⊙O2内切于点P，过点P的直线交⊙O1于点D，交⊙O2于点E；DA与⊙O2相切，切点为C．