题目内容
如图一,三角形ABC中,D、E分别为AB、AC的中点.
问题(1):猜想DE与BC的数量关系;(不必说明理由)
如图二,点O是△ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接.
问题(2):如果DEFG能构成四边形,根据问题(1)的猜想,则四边形DEFG是否为平行四边形,说明理由.
问题(3):当点O移动到△ABC外时,(2)中的结论是否仍然成立?画出图形,不必说明理由.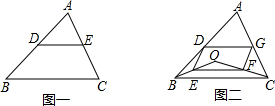
问题(1):猜想DE与BC的数量关系;(不必说明理由)
如图二,点O是△ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接.
问题(2):如果DEFG能构成四边形,根据问题(1)的猜想,则四边形DEFG是否为平行四边形,说明理由.
问题(3):当点O移动到△ABC外时,(2)中的结论是否仍然成立?画出图形,不必说明理由.
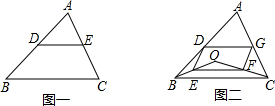
问题(1)根据三角形的中位线定理猜想:DE=
BC;
问题(2)四边形DEFG是平行四边形.
理由如下:∵D、G分别为AB、AC的中点,
∴DG∥BC且DG=
BC,

∵E、F分别为OB、OC的中点,
∴EF∥BC且EF=
BC,
∴DG∥EF且DG=EF,
∴四边形DEFG是平行四边形;
问题(3)如图所示,仍然成立.
| 1 |
| 2 |
问题(2)四边形DEFG是平行四边形.
理由如下:∵D、G分别为AB、AC的中点,
∴DG∥BC且DG=
| 1 |
| 2 |

∵E、F分别为OB、OC的中点,
∴EF∥BC且EF=
| 1 |
| 2 |
∴DG∥EF且DG=EF,
∴四边形DEFG是平行四边形;
问题(3)如图所示,仍然成立.

练习册系列答案
相关题目
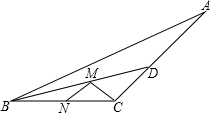 (2013•许昌一模)如图,钝角三角形ABC的面积为15,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为
(2013•许昌一模)如图,钝角三角形ABC的面积为15,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为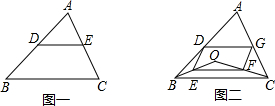 如图一,三角形ABC中,D、E分别为AB、AC的中点.
如图一,三角形ABC中,D、E分别为AB、AC的中点.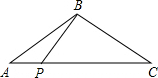 如图,等腰三角形△ABC中,AB=BC,底边AC=8cm,腰长为5cm,一动点P以每秒0.25cm的速度沿底边从点A向点C运动,则点P运动到使PB与一腰垂直时所花的时间是
如图,等腰三角形△ABC中,AB=BC,底边AC=8cm,腰长为5cm,一动点P以每秒0.25cm的速度沿底边从点A向点C运动,则点P运动到使PB与一腰垂直时所花的时间是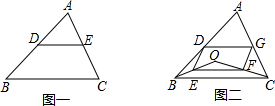 如图一,三角形ABC中,D、E分别为AB、AC的中点.
如图一,三角形ABC中,D、E分别为AB、AC的中点.