题目内容
如图，⊙O1和⊙O2相交于点A、B，过点A的直线分别交两圆于点C、D，点M是CD的中点，直线BM分别交两圆于点E、F．（1）求证：CE∥DF；
（2）求证：ME=MF．
分析：（1）根据圆周角定理及平行线的判定即可得到结论；
（2）证明△CME≌△DMF，根据全等三角形的对应边相等从而得到ME=MF．
（2）证明△CME≌△DMF，根据全等三角形的对应边相等从而得到ME=MF．
解答：
证明：（1）∵连接AB，
∵∠B与∠C是弧AE所对的圆周角，
则∠B=∠C，
∵∠B=∠D，（同弧所对圆周角相等）
∴∠C=∠D．
∴CE∥DF．
（2）∵点M是CD的中点，
∴CM=DM．
在△DFM和△CEM中：
，
∴△CME≌△DMF．（ASA）
∴ME=MF．
证明：（1）∵连接AB，∵∠B与∠C是弧AE所对的圆周角，
则∠B=∠C，
∵∠B=∠D，（同弧所对圆周角相等）
∴∠C=∠D．
∴CE∥DF．
（2）∵点M是CD的中点，
∴CM=DM．
在△DFM和△CEM中：
|
∴△CME≌△DMF．（ASA）
∴ME=MF．
点评：考查了圆周角的定义，平行线的判定，全等三角形的判定和性质的综合运用．
练习册系列答案
相关题目
20、已知：如图，⊙O1和⊙O2相交于A、B两点，动点P在⊙O2上，且在⊙1外，直线PA、PB分别交⊙O1于C、D，问：⊙O1的弦CD的长是否随点P的运动而发生变化？如果发生变化，请你确定CD最长和最短时P的位置，如果不发生变化，请你给出证明．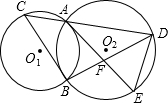
长⊙O1相交于C点，连接BC，过A点作AE∥BC与⊙O相交于E点，与BD相交于F点．
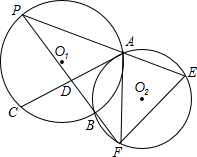、PB的延长线分别交⊙O2于点E、F，PB交AC于D．
16、如图．⊙O1和⊙O2外切于点A，BC是⊙O1和⊙O2的公切线，B、C为切点，求证：AB⊥AC．
（2001•黄冈）已知，如图，⊙O1和⊙O2内切于点P，过点P的直线交⊙O1于点D，交⊙O2于点E；DA与⊙O2相切，切点为C．