题目内容
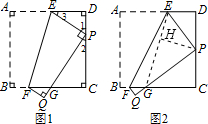
已知正方形纸片ABCD的边长为2.如图,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
(1)求证:△DEP与△CPG相似;
(2)当点P位于CD中点时,求:△DEP与△CPG周长的比;
(3)在(2)的条件下,求证:以P为圆心,以1为半径的圆与直线EG相切.
(1)求证:△DEP与△CPG相似;
(2)当点P位于CD中点时,求:△DEP与△CPG周长的比;
(3)在(2)的条件下,求证:以P为圆心,以1为半径的圆与直线EG相切.

分析:(1)根据题意,∠EPG=90°,可得∠EPD+∠CPG=90°,又∠EPD+∠PED=90°,所以∠CPG=∠PED.加上∠C=∠D,可得△EDP∽△PCG;
(2)根据相似三角形性质求解.因为CP=1,所以需求对应边DE的长度.设DE=x,则AE=EP=2-x,根据勾股定理可求;
(3)连接EG,过P作PH⊥EG交于H,由(2)中的数据利用勾股定理分别求出PG和EG的长,根据直角三角形EPG的面积等于
PE•PG=
PH•EG,从而可求出PH的长为1,恰好为圆的半径,所以以P为圆心,以1为半径的圆与直线EG相切.
(2)根据相似三角形性质求解.因为CP=1,所以需求对应边DE的长度.设DE=x,则AE=EP=2-x,根据勾股定理可求;
(3)连接EG,过P作PH⊥EG交于H,由(2)中的数据利用勾股定理分别求出PG和EG的长,根据直角三角形EPG的面积等于
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:(如图1所示)
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
由折叠知∠EPQ=∠A=90°,
∴∠1+∠3=90°,∠1+∠2=90°,
∴∠2=∠3.
∴△DEP∽△CPG;
(2)解:(如图2所示)
∵四边形ABCD是正方形,AB=2,
∴AB=BC=CD=DA=2.
设AE=x,则ED=2-x,EP=x.
∵P是CD的中点,
∴DP=PC=1.
在Rt△EDP中,∠D=90°,
根据勾股定理得:x2=(2-x)2+1,
解得 x=
,
∴ED=
,
∵△PCG∽△EDP,
∴
=
=
,
∴△DEP与△CPG周长的比是3:4;
(3)证明:连接EG,过P作PH⊥EG交于H,(如图2)
∵△PCG∽△EDP,
∴
=
,
∴
=
,
∴CG=
,
∴PG=
=
,
∵AE=EP=
,
∴EG=
=
,
∴PH=
=
=1,
∴圆心到直线的距离等于1,
∴以P为圆心,以1为半径的圆与直线EG相切.
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
由折叠知∠EPQ=∠A=90°,
∴∠1+∠3=90°,∠1+∠2=90°,
∴∠2=∠3.
∴△DEP∽△CPG;
(2)解:(如图2所示)
∵四边形ABCD是正方形,AB=2,
∴AB=BC=CD=DA=2.
设AE=x,则ED=2-x,EP=x.
∵P是CD的中点,
∴DP=PC=1.
在Rt△EDP中,∠D=90°,
根据勾股定理得:x2=(2-x)2+1,
解得 x=
| 5 |
| 4 |
∴ED=
| 3 |
| 4 |

∵△PCG∽△EDP,
∴
| PC |
| ED |
| ||
| 4 |
| 4 |
| 3 |
∴△DEP与△CPG周长的比是3:4;
(3)证明:连接EG,过P作PH⊥EG交于H,(如图2)
∵△PCG∽△EDP,
∴
| PC |
| DE |
| CG |
| DP |
∴
| 1 | ||
|
| CG |
| 1 |
∴CG=
| 4 |
| 3 |
∴PG=
| CG2+CP2 |
| 5 |
| 3 |
∵AE=EP=
| 5 |
| 4 |
∴EG=
| PE2+PG2 |
| 25 |
| 12 |
∴PH=
| PE•PG |
| EG |
| ||||
|
∴圆心到直线的距离等于1,
∴以P为圆心,以1为半径的圆与直线EG相切.
点评:此题考查了翻折变换、勾股定理及正方形的性质以及相似三角形的判定和性质和圆的切线的判定,综合性较强,解答本题的关键是要求我们熟练勾股定理在解直角三角形中的应用,及翻折变换的性质,难度较大.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点。已知BC=24cm,则这个展开图可折成的正方体的体积为( ) 
| A.64cm3 | B.27cm3 | C.9cm3 | D.8cm3 |
 (2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
(2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.

 如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图可折成的正方体的体积为( )
如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图可折成的正方体的体积为( ) 如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.
如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.