题目内容
(1)如图(1),点C在线段AB上,AC=m,BC=n,点P在经过点C且垂直于AB的直线上,设PC=h,求当h等于多少时,∠APB=90°.(用含m,n的代数式表示h.)
(2)如图(2),△ABC中,AB=AC=5,BC=8,点P是BC上的点,当PB=
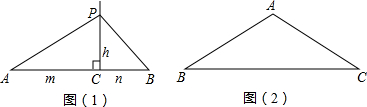
(2)如图(2),△ABC中,AB=AC=5,BC=8,点P是BC上的点,当PB=
4或6.25
4或6.25
时,△ABP是直角三角形.
分析:(1)当PA2+PB2=AB2时,∠APB=90°,再列式得出答案即可;
(2)分两种情况:①∠APB为直角,②∠BAP为直角.
(2)分两种情况:①∠APB为直角,②∠BAP为直角.
解答:解:(1)根据勾股定理及其逆定理,
当PA2+PB2=AB2时,∠APB=90°
即h2+m2+h2+n2=(m+n)2(2分)
从而可得:h=
(2分)
(2)如下图所示:

①当∠APB为直角时,点P为BC的中点,即PB=
BC,
∵BC=8,∴BP=4;
②当∠BAP为直角时,cos∠B=
=
=
,
解得:BP′=6.25.
当PA2+PB2=AB2时,∠APB=90°
即h2+m2+h2+n2=(m+n)2(2分)
从而可得:h=
| mn |
(2)如下图所示:

①当∠APB为直角时,点P为BC的中点,即PB=
| 1 |
| 2 |
∵BC=8,∴BP=4;
②当∠BAP为直角时,cos∠B=
| BP |
| AB |
| AB |
| BP′ |
| 4 |
| 5 |
解得:BP′=6.25.
点评:本题考查勾股定理及等腰三角形的性质,解答第二问要注意分两种情况讨论,不要漏解.

练习册系列答案
相关题目
 如图,数轴上的点A表示的数为a,则a的绝对值等于 ( )
如图,数轴上的点A表示的数为a,则a的绝对值等于 ( ) 如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等.
如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等. 如图,直线DE经过点A,DE∥BC,∠DAB=78°,∠ACF=124°,则∠BAC=
如图,直线DE经过点A,DE∥BC,∠DAB=78°,∠ACF=124°,则∠BAC= 如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中: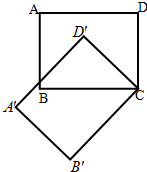 25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题: