题目内容
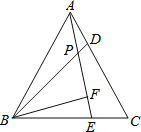
【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
A.2
B.3
C.1
D.8
【答案】A
【解析】
试题分析:证△ABD≌△CAE,推出∠ABD=∠CAE,求出∠BPF=∠APD=60°,得出∠PBF=30°,根据含30度角的直角三角形性质求出即可.
解:∵△ABC是等边三角形,
∴AB=AC.
∴∠BAC=∠C.
在△ABD和△CAE中,
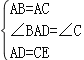 ,
,
∴△ABD≌△CAE(SAS).
∴∠ABD=∠CAE.
∴∠APD=∠ABP+∠PAB=∠BAC=60°.
∴∠BPF=∠APD=60°.
∵∠BFP=90°,∠BPF=60°,
∴∠PBF=30°.
∴PF=![]() .
.
故选;A.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表,根据表中的信息判断,下列结论中错误的是( )
成绩(分) | 30 | 29 | 28 | 26 | 18 |
人数(人) | 32 | 4 | 2 | 1 | 1 |
A. 该班共有40名学生
B. 该班学生这次考试成绩的平均数为29.4分
C. 该班学生这次考试成绩的众数为30分
D. 该班学生这次考试成绩的中位数为28分