题目内容
 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
(1)求证:△CED≌△CFG;
(2)设ED=a,EB=b,问:在线段EF上是否存在点M,EM的长m能使 是方程组
是方程组 的解?若存在,求二次函数
的解?若存在,求二次函数 的最大值或最小值;若不存在,说明理由.
的最大值或最小值;若不存在,说明理由.
(1)证明:∵E、F为AC、BC的中点,
∴EF为△ABC的中位线.
EF∥AB,∠CEF=∠CFE即∠DEC=∠GFC,弧AD=弧BG,∠DCA=∠BCG,
又△ABC为等边三角形,AC=BC则CE=CF,
∴△CED≌△CFG.
(2)解:将 代入
代入 消去p得:
消去p得:
 =0,
=0,
△=1-4×2×[ ],
],
∵△ABC边长为4,EB=b= ,
,
△=1-8×[ ],
],
∴令△≥0,则解得a不符合题意.
∴不存在M点.
分析:(1)本题可以从角边角证明两三角形全等,即∠DEC=∠GFC,∠DCA=∠BCG,CE=CF;
(2)将x、y代入方程组消去p得到关于m的二次方程,用根的判别式判断是否存在M点.
点评:本题考查了几何与函数结合的题型,考查了几何的性质及二次函数的最值.
∴EF为△ABC的中位线.
EF∥AB,∠CEF=∠CFE即∠DEC=∠GFC,弧AD=弧BG,∠DCA=∠BCG,
又△ABC为等边三角形,AC=BC则CE=CF,
∴△CED≌△CFG.
(2)解:将
 代入
代入 消去p得:
消去p得: =0,
=0,△=1-4×2×[
 ],
],∵△ABC边长为4,EB=b=
 ,
,△=1-8×[
 ],
],∴令△≥0,则解得a不符合题意.
∴不存在M点.
分析:(1)本题可以从角边角证明两三角形全等,即∠DEC=∠GFC,∠DCA=∠BCG,CE=CF;
(2)将x、y代入方程组消去p得到关于m的二次方程,用根的判别式判断是否存在M点.
点评:本题考查了几何与函数结合的题型,考查了几何的性质及二次函数的最值.

练习册系列答案
相关题目
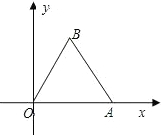 如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线
如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线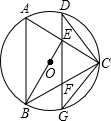 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
 (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长. (2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是
(2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是