题目内容
已知抛物线y1=a1x2+b1x+c1,y2=a2x2+b2x+c2,且满足 .则称抛物线y1,y2互为“友好抛物线”,则下列关于“友好抛物线”的说法不正确的是( )
.则称抛物线y1,y2互为“友好抛物线”,则下列关于“友好抛物线”的说法不正确的是( )A.y1,y2开口方向,开口大小不一定相同
B.y1,y2的对称轴相同
C.如果y1与x轴有两个不同的交点,则y2与x轴也有两个不同的交点
D.如果y2的最大值为m,则y1的最大值为km
【答案】分析:根据题中给出的“友好抛物线”的定义结合二次函数的性质对各选项进行逐一判断即可.
解答:解:A、当a1与a2符号相反时其开口方向相反,当|a1|≠|a2|时,两抛物线开口大小不同,故本选项正确;
B、∵ ,∴-
,∴- =-
=- ,∴y1与y2的对称轴相同,故本选项正确;
,∴y1与y2的对称轴相同,故本选项正确;
C、∵y1与x轴有两个不同的交点,∴△=b12-4a1c1>0,∵抛物线y2中,△=b22-4a2c2=k2(b12-4a1c1)>0,故选项正确;
D、∵如果y2的最值是m,∴y1的最值是 =k•
=k• =km,当k<0时,y1的最小值为km.故选项错误.
=km,当k<0时,y1的最小值为km.故选项错误.
故选D.
点评:本题考查的是二次函数的性质,先根据题意理解“友好抛物线”的定义是解答此题的关键.
解答:解:A、当a1与a2符号相反时其开口方向相反,当|a1|≠|a2|时,两抛物线开口大小不同,故本选项正确;
B、∵
 ,∴-
,∴- =-
=- ,∴y1与y2的对称轴相同,故本选项正确;
,∴y1与y2的对称轴相同,故本选项正确;C、∵y1与x轴有两个不同的交点,∴△=b12-4a1c1>0,∵抛物线y2中,△=b22-4a2c2=k2(b12-4a1c1)>0,故选项正确;
D、∵如果y2的最值是m,∴y1的最值是
 =k•
=k• =km,当k<0时,y1的最小值为km.故选项错误.
=km,当k<0时,y1的最小值为km.故选项错误.故选D.
点评:本题考查的是二次函数的性质,先根据题意理解“友好抛物线”的定义是解答此题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目

 (2013•南昌)已知抛物线yn=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(2013•南昌)已知抛物线yn=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.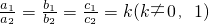 ,则我们称抛物线y1与y2互为“友好抛物线”,请写出当
,则我们称抛物线y1与y2互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标. ,则我们称抛物线y1与y2互为“友好抛物线”,请写出当
,则我们称抛物线y1与y2互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.