题目内容
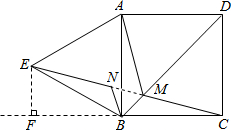
 (2013•怀柔区二模)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,连结AM、CM.
(2013•怀柔区二模)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,连结AM、CM.(1)当M点在何处时,AM+CM的值最小;
(2)当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为
| 3 |
分析:(1)根据“两点之间线段最短”,可得,当M点落在BD的中点时,AM+CM的值最小;
(2)根据“两点之间线段最短”,当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长(如图);
(3)作辅助线,过E点作EF⊥BC交CB的延长线于F,由题意求出∠EBF=30°,设正方形的边长为x,在Rt△EFC中,根据勾股定理求得正方形的边长为
.
(2)根据“两点之间线段最短”,当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长(如图);
(3)作辅助线,过E点作EF⊥BC交CB的延长线于F,由题意求出∠EBF=30°,设正方形的边长为x,在Rt△EFC中,根据勾股定理求得正方形的边长为
| 2 |
解答:解:(1)当M点落在BD的中点时,AM+CM的值最小.
(2)如图,连接CE,当M点位于BD与CE的交点处时,AM+BM+CM的值最小.
理由如下:
∵M是正方形ABCD对角线上一点
∴AM=CM
又AB=BC,BM=BM
∴△ABM≌△CBM
∴∠BAM=∠BCM
又BE=BA=BC
∴∠BEC=∠BCM
∴∠BEC=∠BAM
在EC上取一点N使得EN=AM,连结BN
又∵EB=AB
∴△BNE≌△ABM…(3分)
∴∠EBN=∠ABM,BN=BM
又∵∠EBN+∠NBA=60°
∴∠ABM+∠NBA=60°
即∠NBM=60°
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
(3)过E点作EF⊥BC交CB的延长线于F
∴∠EBF=90°-60°=30°
设正方形的边长为x,则BF=
x,EF=
在Rt△EFC中,
∵EF2+FC2=EC2,
∴(
)2+(
x+x)2=(
+1)2.
解得,x=
(舍去负值).
∴正方形的边长为
.
(2)如图,连接CE,当M点位于BD与CE的交点处时,AM+BM+CM的值最小.
理由如下:
∵M是正方形ABCD对角线上一点
∴AM=CM
又AB=BC,BM=BM
∴△ABM≌△CBM
∴∠BAM=∠BCM
又BE=BA=BC
∴∠BEC=∠BCM
∴∠BEC=∠BAM

在EC上取一点N使得EN=AM,连结BN
又∵EB=AB
∴△BNE≌△ABM…(3分)
∴∠EBN=∠ABM,BN=BM
又∵∠EBN+∠NBA=60°
∴∠ABM+∠NBA=60°
即∠NBM=60°
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
(3)过E点作EF⊥BC交CB的延长线于F
∴∠EBF=90°-60°=30°
设正方形的边长为x,则BF=
| ||
| 2 |
| x |
| 2 |
在Rt△EFC中,
∵EF2+FC2=EC2,
∴(
| x |
| 2 |
| ||
| 2 |
| 3 |
解得,x=
| 2 |
∴正方形的边长为
| 2 |
点评:本题考查轴对称的性质和正方形的性质,是一道综合性的题目,难度较大.

练习册系列答案
相关题目
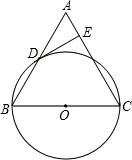 (2013•怀柔区二模)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(2013•怀柔区二模)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.