Question

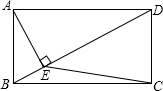矩形ABCD中AE⊥BD于E，AB=4，∠BAE=30°，求△DEC的面积是________．

Answer 1

分析：根据已知条件，先求出线段AE，BE，DE的长度，进而求Rt△AED的面积，再证明△ECD的面积与它相等即可得出答案．
解答：解：如图，过点C作CF⊥BD于F．
∵矩形ABCD中，AB=4，AE⊥BD，∠BAE=30°，
∴AB²=BE×BD，BE=2，AE=2，
∴ED=BD-BE=6，
∴∠ABE=∠CDF=60°，AB=CD=4，AEB=∠CFD=90°．
∴△ABE≌△CDF．
∴AE=CF．
∴S_△AED=ED•AE，S_△ECD=ED•CF
∴S_△AED=S_△CDE，
∵AE=2，DE=6，
∴△ECD的面积是6．
故答案为：6．
点评：本题考查了射影定理及矩形的性质，解题的关键是要注意问题的转化．此题还要求掌握直角三角形的性质，直角三角形中，30°角所对的直角边是斜边的一半．