Question

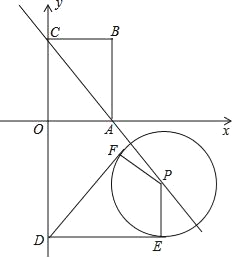
【题目】如图1,在平面直角坐标系中,A(5， 0), B(0， 5), C(2， 0),连AB

(1)如图2，D为第一象限内一点，CDBC于点C,ADAB于点A,求点D坐标；

(2)E为轴负半轴上一动点，连BE，在轴下方做EFBE于点E，并且EF=BE,连FC，直接写出当CF最短时点E的坐标.

Answer 1

【答案】（1）D（7,2）（2）E（-3,0）.

【解析】

(1)如图2，先求出BC、AB直线的解析式，再根据垂直的关系得到直线CD与AD的解析式，联立即可解方程；

（2）如图1，根据题意可知当CF⊥AE时，CF最短，故可证明△OBE≌△CEF，即可求出E点坐标.

（1）∵A(5， 0), B(0， 5), C(2， 0),

求得直线AB的解析式为y=-x+5,

求得直线BC的解析式为y=+5

∵CDBC,ADAB

可设直线CD的解析式为y=x+b，代入C（2,0）得b=-

∴直线CD的解析式为y=x-

设直线AD的解析式为y=x+c，代入A（5,0）得c=-5

∴直线CD的解析式为y=x-5

联立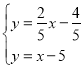，解得

故D（7,2）

（2）根据题意可知当CF⊥AE时，CF最短，故可证明△OBE≌△CEF，即可求出E点坐标.

∵BE⊥EF，∴∠BEO+∠CEF=90°，

又∠BEO+∠EBO=90°，

∴∠CEF =∠OBE

∵BE=EF，

∴△OBE≌△CEF

∴EC=BO=5,

∴OE=5-2=3,

则E（-3,0）.