题目内容
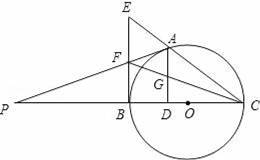
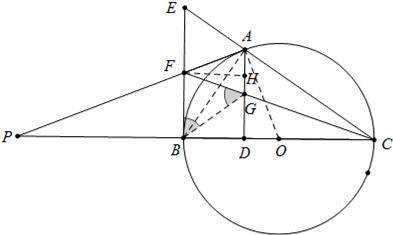
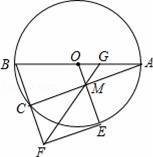
如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=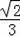
 ;④OC=3
;④OC=3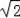
 ,上述结论中正确的有 (填番号).
,上述结论中正确的有 (填番号).

①②④ (填番号).
【考点】圆的综合题.
【分析】①正确,根据AD∥EB得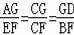
 即可证明.②正确,只要证明∠FAB+∠OAB=90°即可.③错误,求出AH,FH,根据tan∠P=tan∠AFH=
即可证明.②正确,只要证明∠FAB+∠OAB=90°即可.③错误,求出AH,FH,根据tan∠P=tan∠AFH=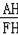
 =
=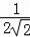
 =
=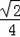
 ,即可解决问题.④正确,在RT△ADO中利用勾股定理即可求出半径.
,即可解决问题.④正确,在RT△ADO中利用勾股定理即可求出半径.
【解答】解:如图连接AO、AB、BG作FH⊥AD于H,
∵EB是切线,AD⊥BC
∴∠EBC=∠ADC=90°,
∴AD∥EB,
∴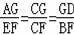
 ,
,
∵AG=GD,
∴EF=FB故①正确,
∵BC是直径,
∴∠BAC=∠BAE=90°,∵EF=FB,
∴FA=FB=FE=FG=3,
∴∠FAB=∠FBA,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠FBA+∠ABO=90°,
∴∠FAB+∠OAB=90°,
∴PA是⊙O的切线,故②正确.
∵FA=FG,FH⊥AG,
∴AH=HG,
∵∠FBD=∠BDH=∠FHD=90°,
∴四边形FBDH是矩形,
∴FB=DH=3,
∵AG=GD,
∴AH=HG=1,GD=2,FH=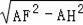
 =2
=2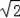
 ,
,
∵FH∥PD,
∴∠AFH=∠APD,
∴tan∠P=tan∠AFH=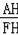
 =
=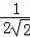
 =
=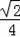
 ,故③错误,
,故③错误,
设半径为r,在RT△ADO中,∵AO2=AD2+OD2,
∴r2=42+(r﹣2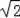
 )2,
)2,
∴r=3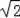
 故④正确,
故④正确,
故答案为①②④.

【点评】本题考查圆的有关知识、平行线分线段成比例定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是添加常用辅助线,体现了转化的思想,把问题转化为方程解决,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
| 成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 2 | 4 | 2 | 5 | 1 |
这此测试成绩的中位数和众数分别为( )
A.47,49 B.47.5,49 C.48,49 D.48,50

 后得到线段CD,则端点C的坐标为( )
后得到线段CD,则端点C的坐标为( )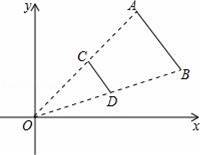








 知
知 ,
, ,则
,则 .
.