题目内容
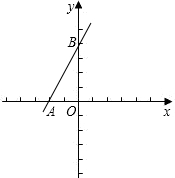 如图,直线y=2x+4与x轴、y轴分别交于A、B两点,把△OAB绕点O顺时针旋转90°得到△OCD.
如图,直线y=2x+4与x轴、y轴分别交于A、B两点,把△OAB绕点O顺时针旋转90°得到△OCD.(1)求经过A、B、D三点的抛物线的解析式;
(2)点P是第一象限内抛物线上一点,是否存在这样的点P,使得点P到直线CD的距离最大?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)根据A、B、D三点的坐标利用待定系数法求出抛物线的解析式;
(2)利用直线CD解析式以及PQ的解析式求出S△PCD=S△PCQ+S△PDQ,得出有关x的解析式,进而求出最值.
(2)利用直线CD解析式以及PQ的解析式求出S△PCD=S△PCQ+S△PDQ,得出有关x的解析式,进而求出最值.
解答:解:(1)∵直线y=2x+4与x轴、y轴分别交于A、B两点,
∴A(-2,0)、B(0,4).
∵△OAB绕点O顺时针旋转90°得到△OCD,
∴C(0,2)、D(4,0),
∴过A、B、D的抛物线解析式为y=-
x2+x+4;
(2)∵C(0,2)、D(4,0),
∴直线CD解析式为y=-
x+2,
设P(x,-
x2+x+4)(0<x<4),
作PE⊥x轴于E,交CD于Q,
则E(x,0),Q(x,-
x+2),
∴PQ=(-
x2+x+4)-(-
x+2)=-
x2+
x+2,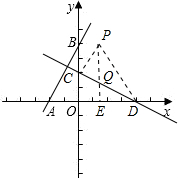
OE=x,DE=4-x,
∴S△PCD=S△PCQ+S△PDQ=
PQ•OE+
PQ•DE=
PQ•OD,
=
(-
x2+
x+2)×4=-x2+3x+4=-(x-
)2+
,
∴当x=
时,△PCD的面积最大,也即P到CD得距离最大.
∴存在点P,使得点P到直线CD的距离最大,此时P点的坐标为(
,
).
∴A(-2,0)、B(0,4).
∵△OAB绕点O顺时针旋转90°得到△OCD,
∴C(0,2)、D(4,0),
∴过A、B、D的抛物线解析式为y=-
| 1 |
| 2 |
(2)∵C(0,2)、D(4,0),
∴直线CD解析式为y=-
| 1 |
| 2 |
设P(x,-
| 1 |
| 2 |
作PE⊥x轴于E,交CD于Q,
则E(x,0),Q(x,-
| 1 |
| 2 |
∴PQ=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |

OE=x,DE=4-x,
∴S△PCD=S△PCQ+S△PDQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 4 |
∴当x=
| 3 |
| 2 |
∴存在点P,使得点P到直线CD的距离最大,此时P点的坐标为(
| 3 |
| 2 |
| 35 |
| 8 |
点评:此题主要考查了二次函数的综合应用,运用待定系数法求二次函数解析式以及在坐标系中求三角形面积是考查重点题型.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
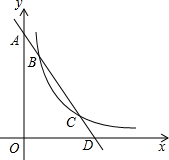 如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线
如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线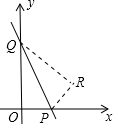 如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是
如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是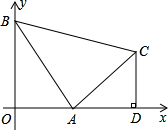 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D. 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F. 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.