题目内容
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列五条结论:
①abc<0;②4ac﹣b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠﹣1)
其中正确的结论是 (把所有正确的结论的序号都填写在横线上)
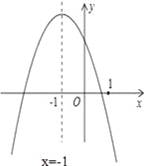

②④⑤
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;二次函数的应用.
【分析】根据抛物线开口方向、对称轴、与y轴交点可判断①;根据抛物线与x轴交点个数可判断②;根据x=0与x=﹣2关于对称轴x=﹣1对称,且x=0时y>0,可判断③;根据x=1时,y<0,且对称轴为x=﹣1可判断④;由抛物线在x=﹣1时有最大值,可判断⑤.
【解答】解:①由抛物线图象得:开口向下,即a<0;c>0,﹣
 =﹣1<0,即b=2a<0,
=﹣1<0,即b=2a<0,
∴abc>0,选项①错误;
②∵抛物线图象与x轴有两个交点,
∴△=b2﹣4ac>0,即4ac﹣b2<0,选项②正确;
③∵抛物线对称轴为x=﹣1,且x=0时,y>0,
∴当x=﹣2时,y=4a﹣2b+c>0,即4a+c>2b,选项③错误;
④∵抛物线对称轴x=﹣1,即﹣
 =﹣1,
=﹣1,
∴a=
 ,
,
由图象可知,当x=1时,y=a+b+c=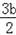
 +c<0,
+c<0,
故3b+2c<0,选项④正确;
⑤由图象可知,当x=﹣1时y取得最大值,
∵m≠﹣1,
∴am2+bm+c<a﹣b+c,即am2+bm+b<a,
∴m(am+b)+b<a,选项⑤正确;
故答案为:②④⑤.
【点评】主要考查图象与二次函数系数之间的关系,掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,则a与b的关系为( ).
,则a与b的关系为( ).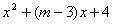 是完全平方式,则m的值等于________.
是完全平方式,则m的值等于________.

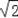
 C.1,1,
C.1,1,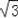
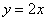 的图像与反比例函数
的图像与反比例函数 的图像没有交点,则实数
的图像没有交点,则实数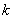 的取值范围在数轴上可表示为 ( )
的取值范围在数轴上可表示为 ( )
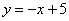 的图像与反比例函数
的图像与反比例函数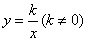 在第一象限内的图像交于
在第一象限内的图像交于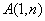 和
和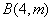 两点.
两点.
 的取值范围.
的取值范围.  = .
= .