题目内容
 如图,点D、E在BC上,∠BDF=∠AEG都是直角,且∠1=∠2.
如图,点D、E在BC上,∠BDF=∠AEG都是直角,且∠1=∠2.
(1)∠2=3∠4,求∠1的度数;
(2)探究∠3与∠4的关系,并说明理由.
解:(1)∵∠AEG=90°,
∴∠2+∠4=90°,
又∵∠2=3∠4,
∴4∠4=90°,
∴∠4=22.5°,
∴∠1=∠2=67.5°;
(2)∵∠BDF=90°,
∴∠1+∠3=90°,
又∵∠2+∠4=90°,∠1=∠2,
∴∠3=∠4.
分析:(1)根据∠AEG=90°可以得到∠2+∠4=90°,再根据∠2=3∠4即可求得∠1的度数;
(2)根据等角的余角相等即可证得.
点评:本题主要考查了角度的计算,并且利用了同角的余角相等这一性质.
∴∠2+∠4=90°,
又∵∠2=3∠4,
∴4∠4=90°,
∴∠4=22.5°,
∴∠1=∠2=67.5°;
(2)∵∠BDF=90°,
∴∠1+∠3=90°,
又∵∠2+∠4=90°,∠1=∠2,
∴∠3=∠4.
分析:(1)根据∠AEG=90°可以得到∠2+∠4=90°,再根据∠2=3∠4即可求得∠1的度数;
(2)根据等角的余角相等即可证得.
点评:本题主要考查了角度的计算,并且利用了同角的余角相等这一性质.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
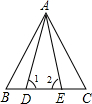 已知:如图,点D、E在BC上,BD=EC,∠1=∠2,求证:AB=AC.
已知:如图,点D、E在BC上,BD=EC,∠1=∠2,求证:AB=AC. 如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:AB=DC.
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:AB=DC. 如图,点E、F在BC上,∠B=∠C,AB=DC,且BE=CF.
如图,点E、F在BC上,∠B=∠C,AB=DC,且BE=CF.
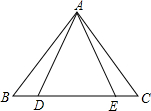 如图,点D、E在BC上,AB=AC,AD=AE.BD和CE有怎样的关系?请说明理由.
如图,点D、E在BC上,AB=AC,AD=AE.BD和CE有怎样的关系?请说明理由.