题目内容
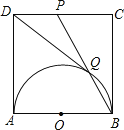
【题目】如图,![]() 经过原点且与两坐标轴分别交于点
经过原点且与两坐标轴分别交于点![]() 和点
和点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,解答下列各题:
,解答下列各题:
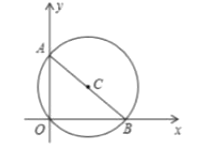
(1)求圆心![]() 的坐标;
的坐标;
(2)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在符合条件的
;(2)存在符合条件的![]() 点:
点:![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)如图(见解析),过![]() 作
作![]() 轴于
轴于![]() ,先确定AB是圆O的直径,再根据垂径定理可得
,先确定AB是圆O的直径,再根据垂径定理可得![]() ,根据中位线定理可知
,根据中位线定理可知![]() ,从而可得点C的坐标;
,从而可得点C的坐标;
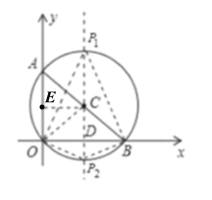
(2)如图(见解析),作![]() 的垂直平分线,交圆
的垂直平分线,交圆![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,根据垂直平分线的性质可知点
,根据垂直平分线的性质可知点![]() 符合要求,再根据圆周角定理和直角三角形的性质求出
符合要求,再根据圆周角定理和直角三角形的性质求出![]() 的度数;最后再分析当OB为所求等腰三角形的腰时点P的位置即可.
的度数;最后再分析当OB为所求等腰三角形的腰时点P的位置即可.
(1)如图,过![]() 作
作![]() 轴于
轴于![]()
![]()
![]()
![]()
∴![]() 是圆
是圆![]() 的直径
的直径
则![]() (垂径定理),
(垂径定理),![]() (中位线定理)
(中位线定理)
即![]() ;
;
(2)如图,作![]() 的垂直平分线,交圆
的垂直平分线,交圆![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]()
则![]() ,
,![]() 都是等腰三角形,即
都是等腰三角形,即![]() 、
、![]() 均符合
均符合![]() 点的要求
点的要求
由垂径定理知:![]() 必过点
必过点![]() ,即
,即![]() 是圆
是圆![]() 的直径
的直径
![]()
∴![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]()
![]()
∴![]()
![]()
同理可得![]()
![]() 是等边三角形
是等边三角形
![]()
故当点P在OB的上方时,不需要考虑OB为腰的情况
又∵![]() 是直径
是直径
![]()
同理可得![]()
故当点P在OB的下方时,OB不可能为腰
综上,存在符合条件的![]() 点:
点:![]() ;
;![]() .
.

练习册系列答案
相关题目