题目内容
直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2= .


40° .
【考点】平行线的性质;三角形内角和定理.
【专题】计算题.
【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4,然后根据对顶角相等解答.
【解答】解:∵l1∥l2,
∴∠3=∠1=85°,
∴∠4=∠3﹣45°=85°﹣45°=40°,
∴∠2=∠4=40°.
故答案为:40°.


【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
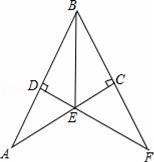
 ,则2a2﹣3bc+4c2的值是 .
,则2a2﹣3bc+4c2的值是 .


 的结果为( )
的结果为( )
 C.
C.





 有意义.
有意义.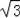
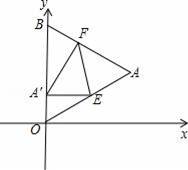
 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
 x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;