题目内容
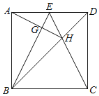
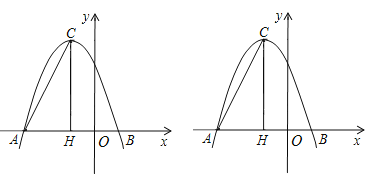
【题目】在平面直角坐标系中,抛物线![]() 与x轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
与x轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写:a= ,b= ,顶点C的坐标为 ;
(2)在y轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
【答案】(1) ![]() ;C(-1,4);
;C(-1,4);
(2)点D(0,3)或(0,1);
(3) ![]() 或
或![]()
【解析】
(1)将A(-3,0)、B(1,0)代入y=ax2+bx+3求出即可,再利用平方法求出顶点坐标即可;
(2)首先证明△CED∽△DOA,得出y轴上存在点D(0,3)或(0,1),即可得出△ACD是以AC为斜边的直角三角形;
(3)首先求出直线CA的解析式为y=k1x+b1,再联立两函数解析式即可得出交点坐标,再利用若点P在对称轴左侧,只能是△PCQ∽△ACH,得∠PCQ=∠ACH得出答案即可.
解:(1)把A(-3,0)、B(1,0)分别代入y=ax2+bx+3,得
![]()
解得![]()
则该抛物线的解析式为:y=-x2-2x+3.
因为y=-x2-2x+3=-(x+1)2+4,
所以顶点C的坐标为(-1,4);
(2)如图1,假设在y轴上存在满足条件的点D,过点C作CE⊥y轴于点E.
由∠CDA=90°得∠1+∠2=90°.
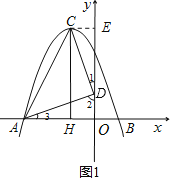
又∵∠2+∠3=90°,
∴∠3=∠1,
又∵∠CED=∠DOA=90°,
∴△CED∽△DOA,
![]()
设D(0,c),
则![]()
变形,得c2-4c+3=0,
解得c1=3,c2=1.
综合上述:在y轴上存在点D(0,3)或(0,1),使△ACD是以AC为斜边的直角三角形.
(3)①若点P在对称轴右侧(如图2),只能是△PCQ∽△CAH,得∠QCP=∠CAH.
延长CP交x轴于M,
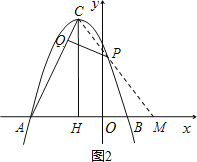
∴AM=CM,
∴AM2=CM2.
设M(m,0),则(m+3)2=42+(m+1)2,
∴m=2,即M(2,0).
设直线CM的解析式为y=k1x+b1,
则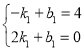
∴直线CM的解析式![]()
联立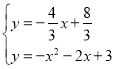
解得 或
或![]() (舍去).
(舍去).
![]()
②若点P在对称轴左侧(如图3),只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.
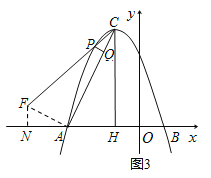
由△CFA∽△CAH得![]()
∴AN=2,FN=1,CH=4,HO=1,则AH=2,
∴点F坐标为(-5,1).
设直线CF的解析式为y=k2x+b2,则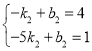
解得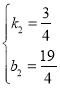
∴直线CF的解析式![]()
联立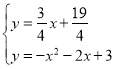
解得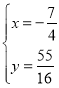 或
或![]() (舍去)
(舍去)
![]()
∴满足条件的点P坐标为![]() 或
或![]()

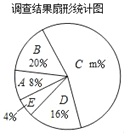
【题目】勤俭节约一直是中华民族的传统美德,某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛,为此先对同学们每月零花钱的数额进行一些了解,随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | a |
C | 60≤x<90 | b |
D | 90≤x<120 | 8 |
E | 120≤x<150 | 2 |
根据以上图表,解答下列问题:
(1)填空:这次调查的同学共有 人,a+b= ,m= ;
(2)求扇形统计图中扇形B的圆心角的度数;
(3)该校共有1200名学生,请估计每月零花钱的数额在60≤x<90范围的人数.