题目内容
【题目】
（1）计算： 
（2）解不等式组：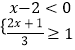 
．
【答案】
（1）解：4cos45°﹣ 
+（π+ 
）0+（﹣1）2
=4× 
﹣2 
+1+1
=2 ﹣2 +2
=2
（2）解： 
，
解不等式①得，x＜2，
解不等式②得，x≥1，
所以不等式组的解集是1≤x＜2
【解析】（1）根据45°角的余弦等于 ，二次根式的化简，任何非0数的0次幂等于1，有理数的乘方进行计算即可得解；（2）先求出两个不等式的解集，再确定这两个解集的公共部分即可．
【考点精析】掌握零指数幂法则和一元一次不等式组的解法是解答本题的根本，需要知道零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．
练习册系列答案
相关题目
