题目内容
【题目】如图，已知：在Rt△ABC中，斜边AB=10，sinA= 
，点P为边AB上一动点（不与A，B重合），PQ平分∠CPB交边BC于点Q，QM⊥AB于M，QN⊥CP于N．
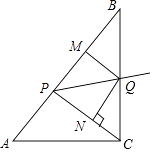
（1）当AP=CP时，求QP；
（2）若四边形PMQN为菱形，求CQ；
（3）探究：AP为何值时，四边形PMQN与△BPQ的面积相等？
【答案】
（1）
解：∵AB=10，sinA= 
，
∴BC=8，
则AC= 
=6，
∵PA=PC．
∴∠PAC=∠PCA，
∵PQ平分∠CPB，
∴∠BPC=2∠BPQ=2∠A，
∴∠BPQ=∠A，
∴PQ∥AC，
∴PQ⊥BC，又PQ平分∠CPB，
∴∠PCQ=∠PBQ，
∴PB=PC，
∴P是AB的中点，
∴PQ= 
AC=3；
（2）
解：∵四边形PMQN为菱形，
∴MQ∥PC，
∴∠APC=90°，
∴ ×AB×CP= ×AC×BC，
则PC=4.8，
由勾股定理得，PB=6.4，
∵MQ∥PC，
∴ 
= 
= 
= 
，即 
= 
，
解得，CQ= 
；
（3）
解：∵PQ平分∠CPB，QM⊥AB，QN⊥CP，
∴QM=QN，PM=PN，
∴S△PMQ=S△PNQ，
∵四边形PMQN与△BPQ的面积相等，
∴PB=2PM，
∴QM是线段PB的垂直平分线，
∴∠B=∠BPQ，
∴∠B=∠CPQ，
∴△CPQ∽△CBP，
∴ 
= 
= 
，
∴ = 
，
∴CP=4× 
=4× 
=5，
∴CQ= 
，
∴BQ=8﹣ = 
，
∴BM= × = 
，
∴AP=AB﹣PB=AB﹣2BM= 
．
【解析】（1）根据正弦的概念求出BC，根据勾股定理求出AC，根据三角形中位线定理计算即可；（2）根据菱形的性质得到MQ∥PC，根据相似三角形的性质列出比例式，计算即可；（3）根据角平分线的性质得到QM=QN，PM=PN，根据题意得到PB=2PM，得到QM是线段PB的垂直平分线，根据垂直平分线的性质、相似三角形的判定定理解答．
【考点精析】本题主要考查了角平分线的性质定理的相关知识点，需要掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上才能正确解答此题．
