题目内容
已知实数a、b满足等式（a2+b2）（a2+b2-2）=8，则a2+b2=________．
4
分析：将a2+b2看作一个整体，然后用换元法解方程即可．
解答：设a2+b2=x，则有：
x（x-2）=8
x2-2x-8=0，
（x+2）（x-4）=0
解得x1=-2，x2=4；
∵a2+b2≥0，
故a2+b2=x2=4；
点评：本题的关键是把a2+b2看成一个整体来计算，即换元法思想．
分析：将a2+b2看作一个整体，然后用换元法解方程即可．
解答：设a2+b2=x，则有：
x（x-2）=8
x2-2x-8=0，
（x+2）（x-4）=0
解得x1=-2，x2=4；
∵a2+b2≥0，
故a2+b2=x2=4；
点评：本题的关键是把a2+b2看成一个整体来计算，即换元法思想．
练习册系列答案
相关题目
，在（2）的条件下，试判断是否存在m的值，使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D，且被x轴截得的劣弧与
是等弧？若存在，求出所有满足条件的m的值；若不存在，说明理由．
，在（2）的条件下，试判断是否存在m的值，使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D，且被x轴截得的劣弧与
是等弧？若存在，求出所有满足条件的m的值；若不存在，说明理由．
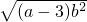+4=2a，则a+b等于多少？