题目内容
如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线．
（1）求∠DOE的度数；
（2）如果∠AOD=51°17′，求∠BOE的度数．
解：（1）∵∠AOC+∠COB=180°，已知OD是∠AOC的平分线，OE是∠COB的平分线，
∴∠DOC=
∠AOC，∠COE=∠COB，
∴∠DOE=∠DOC+∠COE=（∠AOC+∠COB）=90°．
（2）∵∠AOD+∠BOE=90°，∠AOD=51°17′，
∴∠BOE=90°-∠AOD=38°43′．
故答案为90°、38°43′．
分析：（1）由∠AOC+∠COB=180°，又知OD是∠AOC的平分线，OE是∠COB的平分线，故知∠DOE=∠DOC+∠COE=（∠AOC+∠COB），
（2）由∠AOD+∠BOE=90°和∠AOD=51°17′，故能得到∠BOE的度数．
点评：本题主要考查角的比较与运算，还考查了余角的知识点，比较简单．
∴∠DOC=
∠AOC，∠COE=∠COB，∴∠DOE=∠DOC+∠COE=
（∠AOC+∠COB）=90°．（2）∵∠AOD+∠BOE=90°，∠AOD=51°17′，
∴∠BOE=90°-∠AOD=38°43′．
故答案为90°、38°43′．
分析：（1）由∠AOC+∠COB=180°，又知OD是∠AOC的平分线，OE是∠COB的平分线，故知∠DOE=∠DOC+∠COE=
（∠AOC+∠COB），（2）由∠AOD+∠BOE=90°和∠AOD=51°17′，故能得到∠BOE的度数．
点评：本题主要考查角的比较与运算，还考查了余角的知识点，比较简单．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
13、如图，点O在直线AB上，∠COB=∠DOE=90°，那么图中相等的角的对数和互余两角的对数分别为（ ）
如图，点O在直线AB上，且OC⊥OD，若∠COA=36°，则∠DOB的大小为
如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线．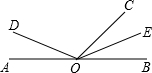
如图，点O在直线AB上，∠AOD=22°30′，∠BOC=45°，OE平分∠BOC，则∠EOC的补角是（ ）