题目内容
【题目】定义：在等腰三角形中，对于顶角的每一个确定的值，其底边与腰的比值都是唯一确定的，这个比值是顶角的正对函数.例如：图①，在△ABC中，AB＝AC，顶角A的正对函数记作sadA，sadA＝
或sadA＝
.
（1）在图①中，若∠B＝60°，则sadA＝ .
（2）如图②，在△ABC中，AB＝AC，若∠BAC＝120°，求sad∠BAC.
（3）在Rt△ABC中，∠C＝90°，sinA＝
，直接写出三个内角的正对函数值.
【答案】（1）1（2）
（3）
， 
， 
．
【解析】试题分析：
(1) 由题意可知△ABC为等边三角形. 等边三角形三边相等，由正对函数的定义知∠A的正对函数值为1.
(2) 要求∠BAC的正对函数值，就是要求线段BC与线段AB或AC的比. 由于题目中没有给出线段长度的具体数值，所以可以将线段AB或AC的长设为2a (其中a>0). 利用BC边上的高AD，通过解Rt△ABD的方式求得线段BD的长. 利用线段BD的长容易得到线段BC的长，进而求得∠BAC的正对函数值.
(3) 要求该直角三角形三个内角的正对函数值，应该以每一个内角为顶角依次构造等腰三角形，求解所构造的等腰三角形的底边和腰的长度，最后根据正对函数的定义得到要求的值.
在构造等腰三角形时，可以在原直角三角形的基础上，通过在适当的边上截取相应的边长即可构造出三个符合要求的等腰三角形.
试题解析：
(1) ∵在△ABC中，AB=AC，
又∵∠B=60°，
∴△ABC是等边三角形，
∴AB=AC=BC.
∴
.
故本题应填写：1.
(2) 
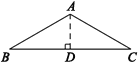
如图，过点A作AD⊥BC，垂足为D.
设AB=AC=2a (a>0).
∵∠BAC=120°，AB=AC，AD⊥BC，
∴在等腰三角形ABC中，BD=CD，∠B=∠C=30°.
∴在Rt△ADB中， 
.
∴CD=BD= 
，
∴
，
∴
.
(3) 
， 
， 
. 具体求解过程如下.
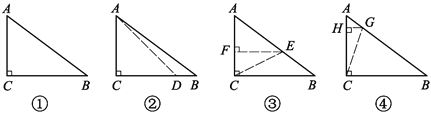
根据题意画出如图①所示的Rt△ABC.
设AB=5a (a>0)，则根据
可知，BC=4a，AC=3a， 
.
下面求解∠C的正对函数值.
如图②，在线段CB上截取CD=CA，则△ACD是以∠C为顶角的等腰三角形.
∵∠C=90°，CD=CA=3a，
∴在Rt△ACD中， 
.
∴
.
下面求解∠A的正对函数值.
如图③，在线段AB上截取AE=AC，则△ACE是以∠A为顶角的等腰三角形.
过点E作EF⊥AC，垂足为F.
∵EF⊥AC，AE=AC=3a，
∴在Rt△AFE中， 
， 
.
∴
，
∴在Rt△CFE中，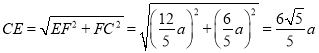 
，
∴
.
下面求解∠B的正对函数值.
如图④，在线段AB上截取BG=BC，则△BCG是以∠B为顶角的等腰三角形.
过点G作GH⊥AC，垂足为H.
∵BG=BC=4a，AB=5a，
∴AG=AB-BG=5a-4a=a.
∵GH⊥AC，AG=a，
∴在Rt△AHG中， 
， 
.
∴
，
∴在Rt△CHG中，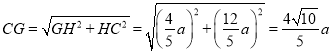 
，
∴
.
