题目内容
 已知,如图:⊙I内切于△ABC,切点分别为D、E、F,若∠C=70°,则∠FDE=
已知,如图:⊙I内切于△ABC,切点分别为D、E、F,若∠C=70°,则∠FDE=
- A.70°
- B.65°
- C.60°
- D.55°
D
分析:D连IF,IE,由切线性质得∠IFC=∠IEC=90°,根据四边形的内角和定理即可求得∠FIE的度数,然后利用圆周角定理即可求得.
解答: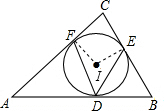 解:连IF,IE,由切线性质得∠IFC=∠IEC=90°,
解:连IF,IE,由切线性质得∠IFC=∠IEC=90°,
∴∠FIE=180°-∠C=110°,
∴∠FDE= FIE=
FIE= ×110°=55°.
×110°=55°.
故选D.
点评:本题考查了切线的性质,以及圆周角定理,正确理解切线的性质,作出辅助线是关键.
分析:D连IF,IE,由切线性质得∠IFC=∠IEC=90°,根据四边形的内角和定理即可求得∠FIE的度数,然后利用圆周角定理即可求得.
解答:
 解:连IF,IE,由切线性质得∠IFC=∠IEC=90°,
解:连IF,IE,由切线性质得∠IFC=∠IEC=90°,∴∠FIE=180°-∠C=110°,
∴∠FDE=
 FIE=
FIE= ×110°=55°.
×110°=55°.故选D.
点评:本题考查了切线的性质,以及圆周角定理,正确理解切线的性质,作出辅助线是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图:⊙I内切于△ABC,切点分别为D、E、F,若∠C=70°,则∠FDE=( )
已知,如图:⊙I内切于△ABC,切点分别为D、E、F,若∠C=70°,则∠FDE=( ) 已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.
已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长. 已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.
已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长. A.70° B.65° C.60° D.55°
A.70° B.65° C.60° D.55°