题目内容
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,AB=2.将三角形ABD沿BD翻折,点A恰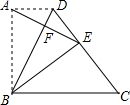 好落在CD边上的点E处,连接AE,交BD于点F.给出下列5个结论:
好落在CD边上的点E处,连接AE,交BD于点F.给出下列5个结论:
①△BCD是等腰三角形;②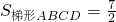 ;③
;③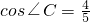 ;④S△EFB=2S△ADE;⑤AE=
;④S△EFB=2S△ADE;⑤AE=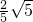 .
.
其中,正确结论的个数为
- A.2个
- B.3个
- C.4个
- D.5个
B
分析:根据折叠的性质得到∠ADB=∠EDB,∠BED=∠BAC=90°,DE=DA=1,AF=EF,BE=BA=2,再由AD∥BC得到∠ADB=∠CBD,则∠CBD=∠BDC,可判断△BCD是等腰三角形;设CE=x,则CB=x+1,利用勾故故定理可得到关于x的方程(x+1)2=22+x2,解得x= ,然后利用梯形的面积公式可计算出S梯形ABCD=
,然后利用梯形的面积公式可计算出S梯形ABCD= (1+
(1+ )×2=
)×2= ;再在Rt△BCE中,利用余弦的定义可计算出cos∠C=
;再在Rt△BCE中,利用余弦的定义可计算出cos∠C=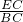 =
=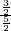 =
= ;易证得Rt△ABF∽Rt△DAF,利用相似的性质得到S△ABF:S△DAF=AB2:AD2=4:1,而S△ABF=S△BEF,S△DAF=S△DEF,则有S△EFB=2S△ADE;最后利用面积法可计算出AE的长为
;易证得Rt△ABF∽Rt△DAF,利用相似的性质得到S△ABF:S△DAF=AB2:AD2=4:1,而S△ABF=S△BEF,S△DAF=S△DEF,则有S△EFB=2S△ADE;最后利用面积法可计算出AE的长为 .
.
解答:∵三角形ABD沿BD翻折,点A恰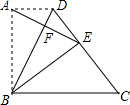 好落在CD边上的点E处,
好落在CD边上的点E处,
∴∠ADB=∠EDB,∠BED=∠BAC=90°,DE=DA=1,AF=EF,BE=BA=2,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠CBD=∠BDC,
∴△BCD是等腰三角形,所以①正确;
设CE=x,则CB=x+1,
在Rt△BCE中,BC2=BE2+CE2,即(x+1)2=22+x2,解得x= ,
,
∴BC=1+x= ,
,
∴S梯形ABCD= (1+
(1+ )×2=
)×2= ,所以②正确;
,所以②正确;
在Rt△BCE中,cos∠C=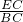 =
=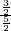 =
= ,所以③错误;
,所以③错误;
∵AF⊥BD,
∴Rt△ABF∽Rt△DAF,
∴S△ABF:S△DAF=AB2:AD2=4:1,
而S△ABF=S△BEF,S△DAF=S△DEF,
∴S△EFB=2S△ADE,所以④正确;
∵S四边形ABED= BD•AE=2S△ABD,
BD•AE=2S△ABD,
而BD=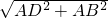 =
= ,
,
∴ ×
× •AE=2×
•AE=2× ×2×1,
×2×1,
∴AE= ,所以⑤错误.
,所以⑤错误.
故选B.
点评:本题考查了折叠的性质:折叠前后两图形全等.也考查了等腰三角形的判定、直角梯形的性质、相似三角形的判定与性质以及勾股定理.
分析:根据折叠的性质得到∠ADB=∠EDB,∠BED=∠BAC=90°,DE=DA=1,AF=EF,BE=BA=2,再由AD∥BC得到∠ADB=∠CBD,则∠CBD=∠BDC,可判断△BCD是等腰三角形;设CE=x,则CB=x+1,利用勾故故定理可得到关于x的方程(x+1)2=22+x2,解得x=
 ,然后利用梯形的面积公式可计算出S梯形ABCD=
,然后利用梯形的面积公式可计算出S梯形ABCD= (1+
(1+ )×2=
)×2= ;再在Rt△BCE中,利用余弦的定义可计算出cos∠C=
;再在Rt△BCE中,利用余弦的定义可计算出cos∠C=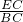 =
=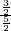 =
= ;易证得Rt△ABF∽Rt△DAF,利用相似的性质得到S△ABF:S△DAF=AB2:AD2=4:1,而S△ABF=S△BEF,S△DAF=S△DEF,则有S△EFB=2S△ADE;最后利用面积法可计算出AE的长为
;易证得Rt△ABF∽Rt△DAF,利用相似的性质得到S△ABF:S△DAF=AB2:AD2=4:1,而S△ABF=S△BEF,S△DAF=S△DEF,则有S△EFB=2S△ADE;最后利用面积法可计算出AE的长为 .
.解答:∵三角形ABD沿BD翻折,点A恰
 好落在CD边上的点E处,
好落在CD边上的点E处,∴∠ADB=∠EDB,∠BED=∠BAC=90°,DE=DA=1,AF=EF,BE=BA=2,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠CBD=∠BDC,
∴△BCD是等腰三角形,所以①正确;
设CE=x,则CB=x+1,
在Rt△BCE中,BC2=BE2+CE2,即(x+1)2=22+x2,解得x=
 ,
,∴BC=1+x=
 ,
,∴S梯形ABCD=
 (1+
(1+ )×2=
)×2= ,所以②正确;
,所以②正确;在Rt△BCE中,cos∠C=
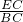 =
=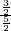 =
= ,所以③错误;
,所以③错误;∵AF⊥BD,
∴Rt△ABF∽Rt△DAF,
∴S△ABF:S△DAF=AB2:AD2=4:1,
而S△ABF=S△BEF,S△DAF=S△DEF,
∴S△EFB=2S△ADE,所以④正确;
∵S四边形ABED=
 BD•AE=2S△ABD,
BD•AE=2S△ABD,而BD=
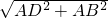 =
= ,
,∴
 ×
× •AE=2×
•AE=2× ×2×1,
×2×1,∴AE=
 ,所以⑤错误.
,所以⑤错误.故选B.
点评:本题考查了折叠的性质:折叠前后两图形全等.也考查了等腰三角形的判定、直角梯形的性质、相似三角形的判定与性质以及勾股定理.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.