题目内容
如图，AB∥EF∥CD，AB=2，CD=8，AE：ED=1：5，则EF的长度为________．
3
分析：过点A作AM∥BC，交EF与点M，交CD于点N．则得到△AEM∽△ADN，根据相似三角形的对应边的比相等即可求解．
解答：
解：过点A作AM∥BC，交EF与点M，交CD于点N．
则NC=MF=AB=2．DN=CD-CN=8-2=6．
∵EF∥CD
∴△AEM∽△ADN
∴
=
=
．
∴EM=DN=1．
∴EF=EM+MF=1+2=3．
点评：本题主要考查了梯形的有关性质，可以通过作腰的平行线转化为三角形的问题解决．
分析：过点A作AM∥BC，交EF与点M，交CD于点N．则得到△AEM∽△ADN，根据相似三角形的对应边的比相等即可求解．
解答：
解：过点A作AM∥BC，交EF与点M，交CD于点N．则NC=MF=AB=2．DN=CD-CN=8-2=6．
∵EF∥CD
∴△AEM∽△ADN
∴
==．∴EM=
DN=1．∴EF=EM+MF=1+2=3．
点评：本题主要考查了梯形的有关性质，可以通过作腰的平行线转化为三角形的问题解决．
练习册系列答案
阅读快车系列答案
相关题目
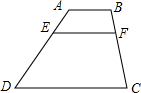如图，AB∥EF∥CD，AB=2，CD=8，AE：ED=1：5，则EF的长度为
如图，AB∥EF，∠B=46°，∠F=54°，则∠BCF=
已知一角的两边与另一个角的两边平行，结合图形，试探索这两个角之间的数量关系．
如图，AB⊥EF，CD⊥EF且AB=CD，则图中全等三角形有
已知：如图，AB∥EF，BC⊥CD，则∠α、∠β、∠γ之间的关系是（ ）