题目内容
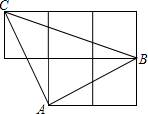 如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,连接AB,BC,CA,则∠ACB的度数为
如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,连接AB,BC,CA,则∠ACB的度数为
- A.30°
- B.45°
- C.60°
- D.75°
B
分析:分别在格点三角形中,根据勾股定理即可得到AB,BC,AC的长度,继而可得出∠ABC的度数.
解答:根据勾股定理可以得到:AC=BC= ,AB=
,AB= ,
,
∵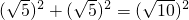 ,即AC2+BC2=AB2,
,即AC2+BC2=AB2,
∴△ABC是等腰直角三角形.
∴∠ACB=45°.
故选B.
点评:本题考查了勾股定理,判断△ABC是等腰直角三角形是解决本题的关键,注意在格点三角形中利用勾股定理.
分析:分别在格点三角形中,根据勾股定理即可得到AB,BC,AC的长度,继而可得出∠ABC的度数.
解答:根据勾股定理可以得到:AC=BC=
 ,AB=
,AB= ,
,∵
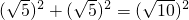 ,即AC2+BC2=AB2,
,即AC2+BC2=AB2,∴△ABC是等腰直角三角形.
∴∠ACB=45°.
故选B.
点评:本题考查了勾股定理,判断△ABC是等腰直角三角形是解决本题的关键,注意在格点三角形中利用勾股定理.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 23、如图,每个小正方形的边长为单位长度1.
23、如图,每个小正方形的边长为单位长度1.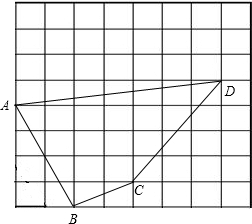 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1.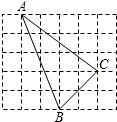 如图,每个小正方形的边长为1,则△ABC的面积等于
如图,每个小正方形的边长为1,则△ABC的面积等于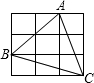 如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为
如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为 如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是
如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是