题目内容
已知:如图,点 是
是 上一点,
上一点, 与
与 是等腰三角形且底边分别为
是等腰三角形且底边分别为 、
、 ,求
,求 的度数。
的度数。

解析考点:等腰三角形的性质;三角形内角和定理。
分析:根据三角形内角和定理可得∠A+∠B+∠ACB=180°,再根据等腰三角形的性质可得∠A+∠B=∠ACB,则可求∠ACB的度数。
解答:
∵△ADC与△BDC是等腰三角形且底边分别为AC、BC,
∴∠A=∠ACD,∠B=∠DCB,
∴∠A+∠B=∠ACB,
∵∠A+∠B+∠ACB=180°,
∴∠ACB=90°。
点评:考查了等腰三角形的性质和三角形内角和定理,得到∠A+∠B=∠ACB是解题的关键。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 31、阅读下面的题目及分析过程,并按要求进行证明.
31、阅读下面的题目及分析过程,并按要求进行证明.

 已知:如图①,点C为线段AB上一点,△ACM和△CBN都是等边三角形,AN,BM交于点P,则△BCM≌△NCA,易证结论:①BM=AN.
已知:如图①,点C为线段AB上一点,△ACM和△CBN都是等边三角形,AN,BM交于点P,则△BCM≌△NCA,易证结论:①BM=AN. (2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.
(2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.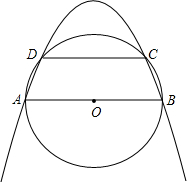 已知:如图,AB是⊙O的直径,CD是⊙O的一条非直径的弦,且AB∥CD,连接AD和BC,
已知:如图,AB是⊙O的直径,CD是⊙O的一条非直径的弦,且AB∥CD,连接AD和BC,