题目内容
在锐角△ABC中，AC=1，AB=c，∠A=60°，△ABC外接圆半径R≤1，则C的取值范围是（ ）
A、
| ||
B、0＜c≤
| ||
| C、c＞2 | ||
| D、c=2 |
分析：由余弦定理求BC，根据：三角形三边关系定理，锐角三角形任意两边的平方和大于第三边的平方，三角形外接圆的直径小于或等于2，列不等式组求解．
解答：解：由余弦定理，得BC=
=
，
依题意，得
?
＜c≤2．
当c=2时，△ABC是直角三角形，因而
＜c＜2．
故选A．
| AB2-2•AB•AC•cosA+AC2 |
| c2-c+1 |
依题意，得
|
| 1 |
| 2 |
当c=2时，△ABC是直角三角形，因而
| 1 |
| 2 |
故选A．
点评：本题考查了三角形外心的性质，三角形三边关系定理，余弦定理的综合运用，特别是锐角三角形任意两边的平方和大于第三边的平方，是理解问题的难点．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
在锐角△ABC中，a、b、c分别表示为∠A、∠B、∠C的对边，O为其外心，则O点到三边的距离之比为（ ）
| A、a：b：c | ||||||
B、
| ||||||
| C、cosA：cosB：cosC | ||||||
| D、sinA：sinB：sinC |
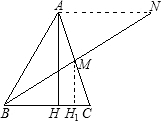在锐角△ABC中，最大的高线AH等于中线BM，求证：∠B＜60°（如图）．
如图，在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①B、E、D、C四点共圆；②AD•AC=AE•AB；③△DEF是等边三角形；④当∠ABC=45°时，BE=
（2013•南开区一模）在锐角△ABC中，∠BAC=60°，BD、CE为高，F是BC的中点，连接DE、EF、FD，则以下结论中一定正确的个数有（ ）