Question

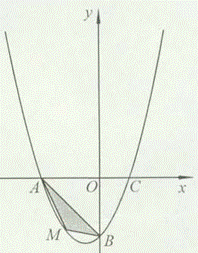
在平面直角坐标系中，已知抛物线经过A(-4，0)，B(0，-4)，C(2，0)三点.

(1)求抛物线的解析式；

(2)若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S.求S关于m的函数关系式，并求出S的最大值；

 (3)若点P是抛物线上的动点，点Q是直线y=－x上的动点，判断有几个位置能使以点P、Q、B、0为顶点的四边形为平行四边形，直接写出相应的点Q的坐标.

Answer 1

 解：（1）设抛物线的解析式为y=ax²+bx+c(a≠0)，则有

        解得

       ∴抛物线的解析式y=x²+x﹣4…………3分

   （2）过点M作MD⊥x轴于点D.设M点的坐标为（m，n）.

        则AD=m+4，MD=﹣n，n=m²＋m－4 .

       ∴S = S_△AMD+S_梯形DMBO－S_△ABO

          = ( m+4) (﹣n)＋(﹣n＋4) (﹣m) －×4×4

          = ﹣2n-2m-8

          = ﹣2(m²＋m－4) -2m-8

          = ﹣m²-4m (－4< m < 0)

∴S最大值 = 4 …………6分

      （3）满足题意的Q点的坐标有四个，分别是：（-4 ，4 ），（4 ，-4），

（-2+，2－），（-2－，2＋）…………14分