Question

在△ABC中，已知AB=AC，∠A=40°，P为AB上一点，∠ACP=20°，则=________．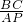

Answer 1

分析：作AD⊥BC于点D，则点D是BC的中点，在△ABC外作∠CAE=20°，则∠BAE=60°，作CE⊥AE，PF⊥AE，从而证明△ACE≌△ACD，结合全等三角形的性质及含30°角直角三角形的性质可得出答案．
解答：作AD⊥BC于点D，则点D是BC的中点，在△ABC外作∠CAE=20°，则∠BAE=60°，

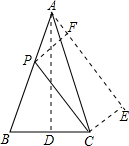
作CE⊥AE，PF⊥AE，则CE=CD（角平分线的性质），
在△ACE和△ACD中，
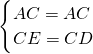
∴△ACE≌△ACD（HL），
所以CE=CD=BC．
又因为PF=PAsin∠BAE=PAsin60=AP，PF=CE，
所以 AP=BC，
因此=．
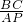故答案为：．
点评：此题考查了全等三角形的判定与性质，解答本题的关键是正确作出辅助线，需要我们熟练全等三角形的判定及30°角直角三角形的性质．