题目内容
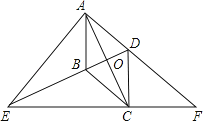
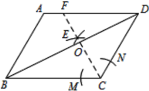
【题目】如图，在平行四边形ABCD中，AB=4，BC=5，∠ABC=60°． 按以下步骤作图：①以C为圆心，以适当长为半径做弧，交CB、CD于M、N两点；②分别以M、N为圆心，以大于
MN的长为半径作弧，两弧相交于点E，作射线CE交BD于点O，交AD边于点F；则BO的长度为（ ）
A.
B.
C.
D.
【答案】C
【解析】
如图（见解析），过点D作
的延长线，垂足为G，先根据作图过程得出CF为
的角平分线，从而可得
，再根据平行四边形的性质、平行线的性质可得
，
，然后利用等腰三角形的性质、直角三角形的性质得出
，
，
，最后根据相似三角形的判定与性质即可得．
如图，过点D作的延长线，垂足为G
由作图过程可知，CF为的角平分线
∴
四边形ABCD是平行四边形
, 
∴，
∴
∴
在
中，
，
∴
在
中，
∴
∵
∴
，即
又
解得
故选：C．
练习册系列答案
相关题目
