题目内容
如图，将平行四边形AEFG变换到平行四边形ABCD，其中E，G分别是AB，AD的中点，下列叙述不正确的是
- A.这种变换是相似变换
- B.对应边扩大到原来的2倍
- C.各对应角度数不变
- D.面积扩大到原来的2倍
D
分析：根据相似多边形对应边之比相等、对应角相等，周长之比等于相似比，而面积之比等于相似比的平方．
解答：平行四边形AEFG变换到平行四边形ABCD，则平行四边形AEFG与平行四边形ABCD相似，因而各对应角度数不变，相似比是1：2，面积的比是1：4，即面积扩大到原来的4倍．故选项D不正确．
故选D．
点评：本题考查相似多边形的性质和相似变换的概念．
分析：根据相似多边形对应边之比相等、对应角相等，周长之比等于相似比，而面积之比等于相似比的平方．
解答：平行四边形AEFG变换到平行四边形ABCD，则平行四边形AEFG与平行四边形ABCD相似，因而各对应角度数不变，相似比是1：2，面积的比是1：4，即面积扩大到原来的4倍．故选项D不正确．
故选D．
点评：本题考查相似多边形的性质和相似变换的概念．
练习册系列答案
相关题目
14、如图，将平行四边形ABCD折叠，使顶点D恰落在AB边上的点M处，折痕为AN，那么对于结论 ①MN∥BC，②MN=AM，下列说法正确的是（ ）
（2012•成都）如图，将平行四边形ABCD的一边BC延长至E，若∠A=110°，则∠1=
（2013•德惠市二模）如图，将平行四边形纸片ABCD沿对角线AC折叠，点D落在点E处，AE恰好过BC边中点，若AB=3，BC=6，则∠B的大小为（ ）
如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处．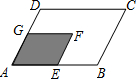
如图，将平行四边形AEFG变换到平行四边形ABCD，其中E，G分别是AB，AD的中点，下列叙述正确的有