题目内容
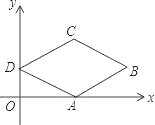
【题目】如图,△ABC的三个顶点分别为A(1,2),B(1,3),C(3,1).若反比例函数y=![]() 在第一象限内的图象与△ABC有公共点,则k的取值范围是( )
在第一象限内的图象与△ABC有公共点,则k的取值范围是( )

A. 2≤k≤3B. 2≤k≤4C. 3≤k≤4D. 2≤k≤3.5
【答案】B
【解析】
根据△ABC三顶点的坐标可知,当k最小是反比例函数过点A,当k取最大值时,反比例函数与直线相切,且切点在线段BC上,由点A的坐标利用反比例函数图象上点的坐标特征可求出k的最小值,再由点B、C的坐标利用待定系数法求出直线BC的解析式,将其代入反比例函数中,令△=0即可求出k的最大值,从而得出结论.
当反比例函数过点A时,k值最小,
此时k=1×2=2;
∵1×3=3×1,
∴反比例函数图象与直线BC的切点在线段BC上,
设直线BC的解析式为y=ax+b,
∴有![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为y=-x+4,
将y=-x+4代入y=![]() 中,得:-x+4=
中,得:-x+4=![]() ,
,
即x2-4x+k=0,
∵反比例函数图象与直线BC只有一个交点,
∴△=(-4)2-4k=0,
解得:k=4.
综上可知:2≤k≤4.
故答案是:2≤k≤4.

练习册系列答案
相关题目