题目内容

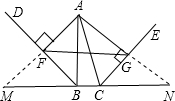
若BD、CE是△ABC的高，BD、CE所在的直线相交所成的角中有一个角为55°，则∠BAC=
125°或55°
125°或55°
．
分析：根据三角形外角的性质及三角形的内角和定理．分∠BAC与这个55°的角在一个四边形内，及∠BAC与这个55°的角不在一个四边形内两种情况讨论．
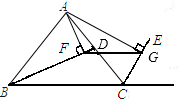
解答：解：若∠BAC与这个55°的角在一个四边形BCDE内，

因为BD、CE是△ABC的高，
∴∠AEB=∠ADC=90°，
∴∠BAE=55°，
∴∠BAC=125°；

若∠BAC与这个50°的角不在一个四边形BCDE内，
因为BD、CE是△ABC的高，
如图：∠BAC=180°-（180°-55°）=55°，
所以∠BAC等于55度．
故答案为：125°或55°．
点评：本题考查四边形内角和定理及三角形的内角和定理．解答的关键是考虑高在三角形内和三角形外两种情况．
练习册系列答案
相关题目
（1）如图所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连接FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG与△ABC的周长之间存在的数量关系是什么？
即：FG=
 
（AB+BC+AC）
（直接写出结果即可）
精英家教网
（2）如图，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与△ABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明．
精英家教网
（3）如图，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与△ABC三边又有怎样的数量关系？直接写出你的猜想即可．不需要证明．答：线段FG与△ABC三边之间数量关系是
 
．
精英家教网
如图1，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F、G，连接FG，延长AF、AG，与直线BC相交于M、N．
（1）试说明：FG=
12
（AB+BC+AC）；
（2）如图2，若BD、CE分别是△ABC的内角平分线，则线段FG与△ABC三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况说明理由；
（3）如图3，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，则线段FG与△ABC三边的数量关系是
 
．
精英家教网
（1）如图所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连接FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG与△ABC的周长之间存在的数量关系是什么？
即：FG=______（AB+BC+AC）
（直接写出结果即可）

（2）如图，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与△ABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明．

（3）如图，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与△ABC三边又有怎样的数量关系？直接写出你的猜想即可．不需要证明．答：线段FG与△ABC三边之间数量关系是______．
（1）如图所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连接FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG与△ABC的周长之间存在的数量关系是什么？
即：FG=______（AB+BC+AC）
（直接写出结果即可）

（2）如图，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与△ABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明．

（3）如图，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与△ABC三边又有怎样的数量关系？直接写出你的猜想即可．不需要证明．答：线段FG与△ABC三边之间数量关系是______．
（1）如图所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连接FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG与△ABC的周长之间存在的数量关系是什么？
即：FG=______（AB+BC+AC）
（直接写出结果即可）

（2）如图，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与△ABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明．

（3）如图，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与△ABC三边又有怎样的数量关系？直接写出你的猜想即可．不需要证明．答：线段FG与△ABC三边之间数量关系是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网