题目内容
如图，函数y=kx+b的图象经过点（-1，2）与（2，-1），当函数值y＞-1时，自变量x的取值范围是________．
x＜2
分析：将点（-1，2）与（2，-1）分别代入函数解析式y=kx+b，即利用待定系数法求得函数y=kx+b；然后根据y＞-1列出关于x的不等式，解不等式即可．
解答：根据题意，得
，
解得，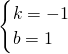
，
∴函数y=kx+b的解析式是函数y=-x+1；
∴当y＞-1时，-x+1＞-1，
解得，x＜2；
故答案是：x＜2．
点评：本题考查了待定系数法求一次函数的解析式、一次函数的性质．要注意利用一次函数的性质，列出方程组，求出k、b值，从而求得其解析式．
分析：将点（-1，2）与（2，-1）分别代入函数解析式y=kx+b，即利用待定系数法求得函数y=kx+b；然后根据y＞-1列出关于x的不等式，解不等式即可．
解答：根据题意，得
，解得，
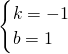，∴函数y=kx+b的解析式是函数y=-x+1；
∴当y＞-1时，-x+1＞-1，
解得，x＜2；
故答案是：x＜2．
点评：本题考查了待定系数法求一次函数的解析式、一次函数的性质．要注意利用一次函数的性质，列出方程组，求出k、b值，从而求得其解析式．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
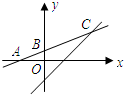如图，函数y=kx+b的图象与x轴，y轴分别交于A（-2，0），B（0，1）两点，那么此函数的图象与函数y=x-1的图象交点C的坐标是
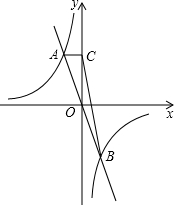如图，函数y=-kx与
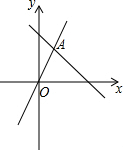（2013•鄞州区模拟）如图，函数y=kx和y=-
如图，函数y=