题目内容
反比例函数y=- 在第二象限的图象上有两点A、B,它们的横坐标分別为-1,-3,直线AB与x轴交于点C,则△AOC的面积为( ).
在第二象限的图象上有两点A、B,它们的横坐标分別为-1,-3,直线AB与x轴交于点C,则△AOC的面积为( ).
A.8 B.10 C.12 D.24
C.
【解析】
试题分析:根据已知点横坐标得出其纵坐标,进而求出直线AB的解析式,求出直线AB与x轴横坐标交点,即可得出△AOC的面积.
试题解析:∵反比例函数y=- 在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3,
在第二象限的图象上有两点A、B,它们的横坐标分别为-1,-3,
∴x=-1,y=6;x=-3,y=2,
∴A(-1,6),B(-3,2),
设直线AB的解析式为:y=kx+b,则
 ,
,
解得: ,
,
则直线AB的解析式是:y=2x+8,
∴y=0时,x=-4,
∴CO=4,
∴△AOC的面积为: ×6×4=12.
×6×4=12.
故选C.
考点:反比例函数系数k的几何意义.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 千克,如果这箱草莓重4.98千克,那么这箱草莓质量 标准.(填“符合”或“不符合”)
千克,如果这箱草莓重4.98千克,那么这箱草莓质量 标准.(填“符合”或“不符合”) BC·r+
BC·r+ AC·r+
AC·r+ AB·r=
AB·r= a·r+
a·r+ b·r+
b·r+ c·r=
c·r= (a+b+c)r
(a+b+c)r

 ,求n的值.
,求n的值.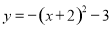 的图像的顶点坐标是( )
的图像的顶点坐标是( )