题目内容
某种饮料分两次提价,提价方案有三种.方案甲是:第一次提价m%,第二次提价n%;方案乙是:第一次提价n%,第二次提价m%;方案丙是:先后提价两次,每次提价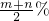 .若m>n>0,则提价最多的方案是
.若m>n>0,则提价最多的方案是
- A.甲
- B.乙
- C.丙
- D.无法确定
C
分析:设单价为1,那么甲售价为:1×(1+m%)(1+n%)=(1+m%)(1+n%);
乙提价后的价格是:(1+n%)(1+m%));
按丙提价方案提价后的价格是:(1+ %)2显然甲、乙两种方案最终价格是一致的,因而只需比较(1+m%)(1+n%)与(1+
%)2显然甲、乙两种方案最终价格是一致的,因而只需比较(1+m%)(1+n%)与(1+ %)2的大小.
%)2的大小.
解答:依题意得:(1+m%)(1+n%)=1+m%+n%+m%•n%=1+(m+n)%+m%•n%;
(1+ %)2=1+(m+n)%+(
%)2=1+(m+n)%+( % )2;
% )2;
所以只要比较m%•n%与( %)2的大小即可
%)2的大小即可
∵( %)2-m%•n%≥0
%)2-m%•n%≥0
∴( %)2≥m%•n%
%)2≥m%•n%
即(1+ %)2>(1+m%) (1+n%)
%)2>(1+m%) (1+n%)
因此,丙种方案提价最多.
故选C.
点评:解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.
需用到的知识点为:(a-b)2≥0.
分析:设单价为1,那么甲售价为:1×(1+m%)(1+n%)=(1+m%)(1+n%);
乙提价后的价格是:(1+n%)(1+m%));
按丙提价方案提价后的价格是:(1+
 %)2显然甲、乙两种方案最终价格是一致的,因而只需比较(1+m%)(1+n%)与(1+
%)2显然甲、乙两种方案最终价格是一致的,因而只需比较(1+m%)(1+n%)与(1+ %)2的大小.
%)2的大小.解答:依题意得:(1+m%)(1+n%)=1+m%+n%+m%•n%=1+(m+n)%+m%•n%;
(1+
 %)2=1+(m+n)%+(
%)2=1+(m+n)%+( % )2;
% )2;所以只要比较m%•n%与(
 %)2的大小即可
%)2的大小即可∵(
 %)2-m%•n%≥0
%)2-m%•n%≥0∴(
 %)2≥m%•n%
%)2≥m%•n%即(1+
 %)2>(1+m%) (1+n%)
%)2>(1+m%) (1+n%)因此,丙种方案提价最多.
故选C.
点评:解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.
需用到的知识点为:(a-b)2≥0.

练习册系列答案
相关题目
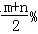 .若m>n>0,则提价最多的方案是
.若m>n>0,则提价最多的方案是