题目内容
 如图,⊙P与x轴相切,与y轴交于点M(0,-2)、N(0,-8),函数
如图,⊙P与x轴相切,与y轴交于点M(0,-2)、N(0,-8),函数 (x>0)的图象经过点P,则k=________.
(x>0)的图象经过点P,则k=________.
-20
分析:过P作MN的垂线,设垂足为A,根据M、N的坐标和垂径定理,易求得AN、OA的长;则PQ=OA,由此可求出P点的纵坐标及⊙P的半径;连接PM,在Rt△PAM中,根据勾股定理,即可求出PA的值,即P点的横坐标,由此可求出P点的坐标,进而求出k即可.
解答: 解:过点P作PA⊥y轴,连接PM;
解:过点P作PA⊥y轴,连接PM;
∵⊙P与x轴相切于点Q
∴PQ⊥x轴,
∵M(0,-2),N(0,-8)
∴OM=2,ON=8,MN=6,
∵PA⊥y轴
∴AN=AM= MN=3
MN=3
∴PQ=OA=5,
在Rt△PAM中,∠PAM=90°,
由勾股定理得:PA= =
= =4,
=4,
∴P点坐标为(4,-5),
∵函数 (x>0)的图象经过点P,
(x>0)的图象经过点P,
∴k=xy=4×(-5)=-20.
故答案为:-20.
点评:此题主要考查了切线的性质、勾股定理、垂径定理等知识的综合应用,根据已知得出AO=PQ是解题关键.
分析:过P作MN的垂线,设垂足为A,根据M、N的坐标和垂径定理,易求得AN、OA的长;则PQ=OA,由此可求出P点的纵坐标及⊙P的半径;连接PM,在Rt△PAM中,根据勾股定理,即可求出PA的值,即P点的横坐标,由此可求出P点的坐标,进而求出k即可.
解答:
 解:过点P作PA⊥y轴,连接PM;
解:过点P作PA⊥y轴,连接PM;∵⊙P与x轴相切于点Q
∴PQ⊥x轴,
∵M(0,-2),N(0,-8)
∴OM=2,ON=8,MN=6,
∵PA⊥y轴
∴AN=AM=
 MN=3
MN=3∴PQ=OA=5,
在Rt△PAM中,∠PAM=90°,
由勾股定理得:PA=
 =
= =4,
=4,∴P点坐标为(4,-5),
∵函数
 (x>0)的图象经过点P,
(x>0)的图象经过点P,∴k=xy=4×(-5)=-20.
故答案为:-20.
点评:此题主要考查了切线的性质、勾股定理、垂径定理等知识的综合应用,根据已知得出AO=PQ是解题关键.

练习册系列答案
相关题目
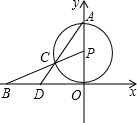 轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.
轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.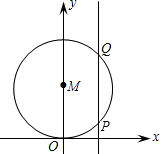 如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方.若P点的坐标是(2,1),求圆心M的坐标.
如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方.若P点的坐标是(2,1),求圆心M的坐标. 如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是
如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是 (2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是
(2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是 (2012•黔西南州模拟)如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(
(2012•黔西南州模拟)如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(