Question

在任意四边形ABCD中，E、F、G、H分别为各边中点，则四边形EFGH一定为________．

Answer 1

平行四边形
分析：在任意四边形ABCD中，E、F、G、H分别为各边中点，当连接四边形的对角线时，可以知道E、F、G、H连接任意两点均为两条对角线与两边组成三角形的中位线，可以得出答案，为平行四边形．
解答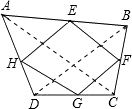：解：如图所示：
连接AC、BD，
∵E、F、G、H分别为各边中点，
∴EH、EF、FG、GH均为中位线，
∴EH∥BD且EF=BD，GF∥BD且GF=BD，
∴EH∥GF且EH=GF，
∴四边形EFGH为平行四边形．
故答案为：平行四边形．
点评：本题考查了平行四边形的判定，有几种判定方法：
①两组对边分别平行的四边形是平行四边形；
②一组对边平行且相等的四边形是平行四边形；
③两组对边分别相等的四边形是平行四边形；
④两条对角线互相平分的四边形是平行四边形；
⑤两组对角分别相等的四边形是平行四边形．