题目内容
甲、乙两名跳高运动员,10次跳高成绩如下:| 甲 | 2 | 2.1 | 1.8 | 1.7 | 1.9 | 2.4 | 1.7 | 1.8 | 2.3 | 2.3 |
| 乙 | 2.2 | 2.2 | 2 | 1.9 | 1.8 | 1.7 | 1.8 | 2.3 | 1.9 | 2.3 |
分析:要比较甲乙中哪个运动员发挥比较稳定,需计算并比较它们的方差.先计算其平均数,根据方差的计算方法计算方差,进行比较可得结论.
解答:解:甲的平均数为
(2+2.1+1.8+1.7+1.9+2.4+1.7+1.8+2.3+2.3)=2;
乙的平均数为
(2.2+2.2+2+1.9+1.8+1.7+1.8+2.3+1.9+2.3)=2;
甲的方差为
(0.01+0.04+0.09+0.01+0.16+0.09+0.04+0.09+0.09)=0.062;
乙的方差为
(0.04+0.04+0.01+0.04+0.09+0.04+0.09+0.09+0.09)=0.0449;
分析可得:甲、乙运动员的平均成绩都是2,而甲、乙的方差分别为0.062和0.0449,
即乙的方差小于甲的方差,所以乙运动员发挥比较稳定.
| 1 |
| 10 |
乙的平均数为
| 1 |
| 10 |
甲的方差为
| 1 |
| 10 |
乙的方差为
| 1 |
| 10 |
分析可得:甲、乙运动员的平均成绩都是2,而甲、乙的方差分别为0.062和0.0449,
即乙的方差小于甲的方差,所以乙运动员发挥比较稳定.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
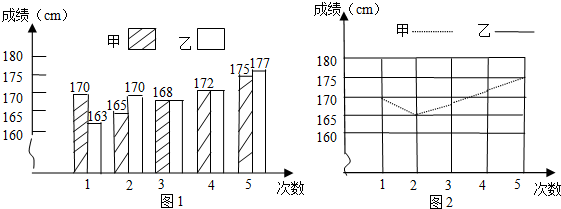
某校拟派一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔比赛,他们的成绩(单位:米)如下:
(1)要评价这两位运动员的平均水平,你选择什么统计量?求出这个统计量.
(2)请求出两组数据的方差,这两个方差的大小反映了什么?
(3)经预测,跳高1.65米就很肯获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员比赛?若预测跳高1.70米可获得冠军呢?
| 甲 | 1.70 | 1.65 | 1.68 | 1.69 | 1.72 | 1.73 | 1.68 | 1.67 |
| 乙 | 1.60 | 1.73 | 1.72 | 1.61 | 1.62 | 1.71 | 1.70 | 1.75 |
(2)请求出两组数据的方差,这两个方差的大小反映了什么?
(3)经预测,跳高1.65米就很肯获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员比赛?若预测跳高1.70米可获得冠军呢?