题目内容
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求tan∠OCE的值.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求tan∠OCE的值.考点:垂径定理,解直角三角形
专题:
分析:先根据垂径定理求出CE的长,再根据勾股定理求出OE的长,根据锐角三角函数的定义即可得出结论.
解答:解:∵AB是⊙O的直径,AB=10,
∴OC=5.
∵弦CD⊥AB,CD=8,
∴CE=4,
∴OE=
=
=3,
∴tan∠OCE=
=
.
∴OC=5.
∵弦CD⊥AB,CD=8,
∴CE=4,
∴OE=
| OC2-CE2 |
| 52-42 |
∴tan∠OCE=
| OE |
| CE |
| 3 |
| 4 |
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
下列运动形式属于旋转的是( )
| A、钟表上钟摆的摆动 |
| B、投篮过程中球的运动 |
| C、“神十”火箭升空的运动 |
| D、传动带上物体位置的变化 |
已知等腰三角形的一内角度数为40°,则它的底角的度数为( )
| A、100° |
| B、70° |
| C、40°或70° |
| D、40°或100° |
在比例尺是1:8000的淮北市城区地图上,淮海路的长度约为25cm,它的实际长度约为( )
| A、2000m |
| B、2000cm |
| C、3200m |
| D、3200cm |
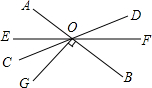 如图,已知直线AB、CD、EF相交于点O,GO⊥AB,∠DOB是它余角的2倍.∠AOE=2∠DOF.
如图,已知直线AB、CD、EF相交于点O,GO⊥AB,∠DOB是它余角的2倍.∠AOE=2∠DOF. 如图,已知直线a∥b,直线c分别与直线a,b相交于点A和点B,图中一组同旁内角的平分线相交于点C,已知三角形的内角和等于180°,求∠C的度数.
如图,已知直线a∥b,直线c分别与直线a,b相交于点A和点B,图中一组同旁内角的平分线相交于点C,已知三角形的内角和等于180°,求∠C的度数. 如图,AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明理由.
如图,AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明理由. 如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.