题目内容
【题目】在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.

(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
【答案】(1)![]() ,
,![]() ;(2)CQ
;(2)CQ![]() 或CQ
或CQ![]() ;(3)
;(3)![]() 或
或![]()
【解析】
试题分析:(1)先根据勾股定理求得BC的长,再结合点D为BC的中点可得CD的长,然后证得△ABC∽△DEC,根据相似三角形的性质即可求得结果;
(2)分①当点P在AB边上时,②当点P在AB的延长线上时,根据相似三角形的性质求解即可;
(3)由△BPD∽△EQD可得![]() ,若设BP=x ,则
,若设BP=x ,则![]() ,
,![]() ,可得
,可得![]() ,即得∠QPD=∠C,又可证∠PDE=∠CDQ,则可得△PDF∽△CDQ,再分①当CQ=CD时,②当QC=QD时,③当DC=DQ时,三种情况,根据等腰三角形的性质求解即可.
,即得∠QPD=∠C,又可证∠PDE=∠CDQ,则可得△PDF∽△CDQ,再分①当CQ=CD时,②当QC=QD时,③当DC=DQ时,三种情况,根据等腰三角形的性质求解即可.
(1)在Rt△ABC中,∠A=90°,AB=6,AC=8
∴BC=10
点D为BC的中点
∴CD=5
可证△ABC∽△DEC
∴![]() , 即
, 即![]()
∴![]() ,
,![]() ;
;
(2)①当点P在AB边上时,在Rt△ABC中,∠B+∠C=90°,
在Rt△EDC中,∠DEC+∠C=90°,
∴∠DEC=∠B
∵DE⊥BC,∠PDQ=90°
∴∠PDQ=∠BDE=90°
∴∠BDP=∠EDQ
∴△BPD∽△EQD
∴![]() ,即
,即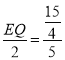 ,
,
∴![]()
∴CQ=EC-EQ![]() ;
;
②当点P在AB的延长线上时,同理可得:![]() ,
,
∴CQ=EC+EQ![]() ;
;
(3)∵线段PQ与线段DE的交点为点F,
∴点P在边AB上
∵△BPD∽△EQD
∴![]()
若设BP=x ,则![]() ,
,![]() ,可得
,可得![]()
∴∠QPD=∠C
又可证∠PDE=∠CDQ
∴△PDF∽△CDQ
∵△PDF为等腰三角形
∴△CDQ为等腰三角形
①当CQ=CD时,可得![]() ,解得
,解得![]()
②当QC=QD时, 过点Q作QM⊥CB于M,
∴![]() ,
,![]()
∴![]() ,解得
,解得![]()
③当DC=DQ时,过点D作DN⊥CQ于N,
∴![]() ,
,![]()
∴![]() ,解得
,解得![]() (不合题意,舍去)
(不合题意,舍去)
∴综上所述,![]() 或
或![]() .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案