题目内容
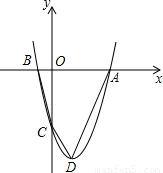
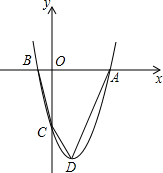 如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程
如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程| 1 |
| 2 |
(1)求这条抛物线的表达式;
(2)填空:(1)问题中抛物线先向上平移3个单位,再向右平移2个单位,得到的抛物线是
y=(x-3)2-6
y=(x-3)2-6
;(3)在第一象限内,问题(1)中的抛物线上是否存在点P,使S△ABP=
| 1 |
| 5 |
分析:(1)设此抛物线的表达式为y=ax2+bx+c,令y=0,求出x的值,即可以求出点A和点B的坐标,列出a、b、c的方程组,求出a、b、c即可;
(2)根据平移“上加下减,左加右减”的规律进行作答;
(3)首先根据(1)求出的解析式求出D点的坐标,过点D作DE⊥x轴,垂足为E,设点P的坐标为(m,n),根据四边形和三角形面积之间的关系,求出n的值,进而求出P点的坐标.
(2)根据平移“上加下减,左加右减”的规律进行作答;
(3)首先根据(1)求出的解析式求出D点的坐标,过点D作DE⊥x轴,垂足为E,设点P的坐标为(m,n),根据四边形和三角形面积之间的关系,求出n的值,进而求出P点的坐标.
解答: 解:(1)设此抛物线的表达式为y=ax2+bx+c
解:(1)设此抛物线的表达式为y=ax2+bx+c
由
x2-x-4=0得(x-4)(x+2)=0
∵x1>x2,
∴x1=4,x2=-2
∴点A的坐标为(4,0),点B的坐标为(-2,0)
∵抛物线经过点C(0,-8),
∴c=-8
又∵抛物线经过A、B两点,
∴
解得:a=1,b=-2,
故设此抛物线的表达式为y=x2-2x-8;
(2)y=(x-3)2-6 或y=x2-6x+3;
(3)存在
由y=x2-2x-8得y=(x-1)2-9,
点D的坐标是(1,-9),
过点D作DE⊥x轴,垂足为E,设点P的坐标为(m,n),
∵S四边形ABCD=S△OBC+S梯形EOCD+S△EAD=
×2×8+
×(9+8)×1+
×3×9=8+
+
=30…(7分)S△PAB=
×6×n=3n
又∵S△PAB=
S四边形ABCD
∴3n=
×30,
∴n=2,
∵点P在抛物线上,
∴x2-2x-8=2,
解得:x1=1+
,x2=1-
(舍去)
故点P的坐标为(1+
,2).
 解:(1)设此抛物线的表达式为y=ax2+bx+c
解:(1)设此抛物线的表达式为y=ax2+bx+c由
| 1 |
| 2 |
∵x1>x2,
∴x1=4,x2=-2
∴点A的坐标为(4,0),点B的坐标为(-2,0)
∵抛物线经过点C(0,-8),
∴c=-8
又∵抛物线经过A、B两点,
∴
|
解得:a=1,b=-2,
故设此抛物线的表达式为y=x2-2x-8;
(2)y=(x-3)2-6 或y=x2-6x+3;
(3)存在
由y=x2-2x-8得y=(x-1)2-9,
点D的坐标是(1,-9),
过点D作DE⊥x轴,垂足为E,设点P的坐标为(m,n),
∵S四边形ABCD=S△OBC+S梯形EOCD+S△EAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 2 |
| 27 |
| 2 |
| 1 |
| 2 |
又∵S△PAB=
| 1 |
| 5 |
∴3n=
| 1 |
| 5 |
∴n=2,
∵点P在抛物线上,
∴x2-2x-8=2,
解得:x1=1+
| 11 |
| 11 |
故点P的坐标为(1+
| 11 |
点评:本题主要考查二次函数的综合题的知识,解答本题的关键是掌握二次函数的性质和平移的知识,特别是第三问需要弄清楚四边形和三角形之间的面积关系,此题难度较大.

练习册系列答案
相关题目
 如图,抛物线过点O(0,0),A(3,3)和B(4,0).
如图,抛物线过点O(0,0),A(3,3)和B(4,0). 如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程
如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程 x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点.
x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点. S四边形ABCD.
S四边形ABCD.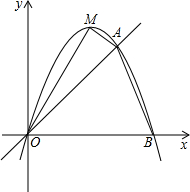 如图,抛物线过点O(0,0),A(3,3)和B(4,0).
如图,抛物线过点O(0,0),A(3,3)和B(4,0). x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点.
x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点. S四边形ABCD.
S四边形ABCD.