题目内容
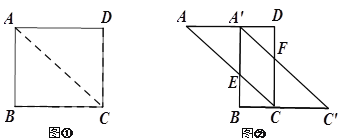
【题目】如图①,已知AC是矩形纸片ABCD的对角线,AB =3,BC =4.现将矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图②中△A′BC′,当四边形A′ECF是菱形时,平移距离AA′的长是___________.
【答案】2.5
【解析】由矩形的性质求得AC=5,由平移的性质求得A/B=DC=3,设AA/=x,则A/D=4-x,由菱形的性质得出A/E∥FC,A/E=EC,由平行线的性质得出△AA/E∽△ADC,由相似的性质得出![]() =
=![]() =
=![]() ,求出AE=
,求出AE=![]() x,A′E=
x,A′E=![]() x,EC=AC-AE=5-
x,EC=AC-AE=5-![]() x,得出
x,得出![]() x=5-
x=5-![]() x,求出x即可得出结果.
x,求出x即可得出结果.
解:∵矩形纸片ABCD,AB =3,BC =4
∴在图②中,AD=4,A′B=DC=3,AC=![]() ,
,
设A A′=x,∴A′D=4-x,
∵四边形A′ECF是菱形,
∴A/E∥FC,A/E=EC,
∴△AA/E∽△ADC,由相似的性质得出![]() =
=![]() =
=![]() ,
,
AE=![]() x,A′E=
x,A′E=![]() x,EC=AC-AE=5-
x,EC=AC-AE=5-![]() x,
x,
∴![]() x=5-
x=5-![]() x,
x,
解得:x=2.5.
故答案为:2.5.
“点睛”本题考查了矩形的性质、勾股定理、平移的性质、菱形的性质三角形相似的判定与性质等知识;熟练掌握三角形相似的判定与性质是解决问题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目