题目内容
 如图,已知∠AOC与∠BOD有公共顶点O,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.
如图,已知∠AOC与∠BOD有公共顶点O,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.分析:求出∠BOM+∠CON=α-β,根据角平分线定义得出∠AOB=2∠BOM,∠COD=2∠CON,求出∠AOB+∠COD=2(∠BOM+∠CON)=2α-2β,代入∠AOD=∠AOB+∠COD+∠BOC求出即可.
解答:解:∵∠MON=α,∠BOC=β,
∴∠BOM+∠CON=α-β,
∵OM平分∠AOB,ON平分∠COD,
∴∠AOB=2∠BOM,∠COD=2∠CON,
∴∠AOB+∠COD=2(∠BOM+∠CON)=2α-2β,
∴∠AOD=∠AOB+∠COD+∠BOC=2α-2β+α=3α-2β.
∴∠BOM+∠CON=α-β,
∵OM平分∠AOB,ON平分∠COD,
∴∠AOB=2∠BOM,∠COD=2∠CON,
∴∠AOB+∠COD=2(∠BOM+∠CON)=2α-2β,
∴∠AOD=∠AOB+∠COD+∠BOC=2α-2β+α=3α-2β.
点评:本题考查了角的有关计算和角平分线定义的应用,主要考查学生的计算能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线.
如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线. 如图,已知∠AOC与∠AOB互为补角,OM、ON分别是∠AOC、∠AOB的平分线,且∠MON=35°,求∠COB的补角和∠AON的余角.
如图,已知∠AOC与∠AOB互为补角,OM、ON分别是∠AOC、∠AOB的平分线,且∠MON=35°,求∠COB的补角和∠AON的余角.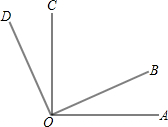 如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
如图,已知∠AOC与∠BOD都是直角,∠BOC=65° 如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
如图,已知∠AOC与∠BOD都是直角,∠BOC=65°