题目内容
已知平面内有一点P，它的横坐标与纵坐标互为相反数，且与原点的距离是2，则P点的坐标为
- A.（-1，1）或（1，-1）
- B.（1，-1）
- C.（-
，）或（，-） - D.（，-）
C
分析：根据勾股定理知识解答．
解答：设点P的横坐标与纵坐标分别为x、-x，
所以x2+（-x）2=22，
解得，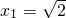
，
，
所以
，
，
所以P点的坐标为（，-），（-，）．
故选C．
点评：本题考查了平面直角坐标系中两点间的距离公式，注意由于点P所在的象限不确定，所以其坐标有两解．
分析：根据勾股定理知识解答．
解答：设点P的横坐标与纵坐标分别为x、-x，
所以x2+（-x）2=22，
解得，
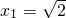，，所以
，，所以P点的坐标为（
，-），（-，）．故选C．
点评：本题考查了平面直角坐标系中两点间的距离公式，注意由于点P所在的象限不确定，所以其坐标有两解．
练习册系列答案
相关题目
已知平面内有两点A（-1，3）、B（2，1），x轴上有一点P满足PA+PB的值最小，请在x轴上标出点P的位置，并求出点P的坐标．已知平面内有一点P，它的横坐标与纵坐标互为相反数，且与原点的距离是2，则P点的坐标为（ ）
| A、（-1，1）或（1，-1） | ||||||||
| B、（1，-1） | ||||||||
C、（-
| ||||||||
D、（
|
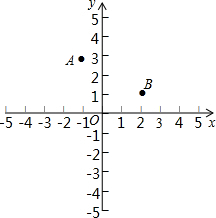已知平面内有两点A（-1，3）、B（2，1），x轴上有一点P满足PA+PB的值最小，请在x轴上标出点P的位置，并求出点P的坐标．